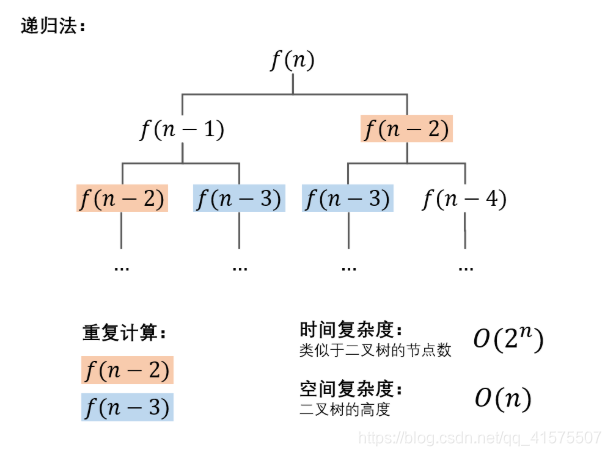
1、斐波那契数列的递归求法(不推荐使用,一般都会超时): 原理:把fib(n) 问题的计算拆分成 fib(n-1)和fib(n−2) 两个子问题的计算,并递归,以 f(0) 和 f(1) 为终止条件。 缺点:需要大量的递归计算,用该很容易超时。 2、记忆化递归法(以空间换时间的方法): 原理:在递归法的基础上,新建一个长度为 n 的数组,用于在递归时存储 f(0) 至 f(n) 的数字值,重复遇到某数字则直接从数组取用,避免了重复的递归计算。因为fib(n)的n是一定的,无论调用多少次都会得到相同的结果。比如我们求fib(10),如果使用上面的递归方式会多次调用fib(7)。如果我们用一个数组将fib(7)的结果存起来,那么当再需要用fib(7)的时候直接使用就可以了,就不需要重复计算,这时候时间复杂度就得到了极大的优化降到了O(n)。 缺点:因为需要开一个数组,长度为n,空间复杂度较高。但是将这两种一块运行比较,你会发现当n比较大的时候,这两种方法得出结果的时间相差很大。 3、优化后的动态规划算法(以时间换空间的方法): 原理:由于斐波那契数列第 n 项只与第 n−1 和第 n−2 项有关,因此只需要初始化三个整形变量 sum,a,b,利用辅助变量 sum 使 a,b 两数字交替前进即可。 时间复杂度:O(n) 原因:计算fib(n)要循环 n 次,每次循环内的计算操作时间复杂度为O(1) 空间复杂度:只需要定义几个变量,因此空间复杂度为O(1) 4、循环求余法以及大数的处理: 相关题目练习:力扣 面试题10- I. 斐波那契数列
#include<iostream> using namespace std; long fib(int n){ if(n==0 || n==1){ return n; } return fib(n-1)+fib(n-2); } int main(){ int n; cin>>n; cout<<fib(n); }
#include<iostream> using namespace std; //申请一个足够大的数组 long memo[1000000] = {0}; long memo2[1000000] = {0}; //写法1: long fib(int n){ if(n==0 || n==1){ return n; } if(memo[n] != 0){ return memo[n]; //如果计算过,就返回 } //没有计算过则继续算 return memo[n] = fib(n-1) + fib(n-2); } //写法2: long fib2(int n){ if(n==0 || n==1){ return n; } if(memo2[n] == 0){ memo2[n] = fib2(n-1) + fib2(n-2); } return memo2[n]; } int main(){ int n; cin>>n; cout<<fib(n)<<endl; cout<<fib2(n); return 0; }
#include<iostream> using namespace std; long fib(int n){ int a = 0,b = 1; long sum; for(int i=0;i<n;i++){ sum = a + b; a = b; b = sum; } return a; //注意应该return a;而不是sum,sum是fib(n+1) } int main(){ int n; cin>>n; cout<<fib(n); return 0; }
#include<iostream> using namespace std; long fib(int n){ int a = 0,b = 1; long sum; for(int i=0;i<n;i++){ sum = (a + b)%1000000007; a = b; b = sum; } return a; //注意应该return a;而不是sum,sum是fib(n+1) } int main(){ int n; cin>>n; cout<<fib(n); return 0; }
class Solution { public: int fib(int n) { int a = 0,b = 1,sum; for(int i=0;i<n;i++){ sum = (a + b) % 1000000007; a = b; b = sum; } return a; } };
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)