本文为博主原创文章,未经博主允许不得转载 计算2D空间气流气压要用到以下方程式: 其中第一个方程为 对第一节中的三个方程进行时间离散化(Temporal Discretization)和空间离散化(Spatial Discretization)。其中时间离散化选用前进差分(Forward Difference),对于空间离散化,一阶偏微分(如: 离散化之后的方程如下: 关于计算网格请看下图说明: 接着我们将离散化后的方程式的n+1时点项和n时点项分离,n+1时点项放在等式左边,n时点项放在等式右边。变形后的结果如下: 假设我们模拟下图所示二维房间的气流。房间的左右侧完全开敞,无墙壁等物体;上下侧为固体墙壁。风从左侧流入房间,从右侧流出。 假设房间最开始 根据3.1节的模拟条件,选用如下图所示边界条件。 根据以上公式和模拟条件,就可以开始编写Python程序啦。 感谢您阅读本文,如您对本文有任何疑问,或者发现本文有任何错误之处,欢迎您联系我。
1.模拟二维空间气流气压用到的方程式
x方向速度
u的N-S方程式(Navier-Stokes equation);第二个方程为
y方向速度
v的N-S方程式(Navier-Stokes equation);第三个方程为第一二个方程进行数学变换得到的方程。第三个方程将气压
p与速度关联起来,称为气压的泊松方程。

记号:
u:
x方向速度
[m/s]
v:
y方向速度
[m/s]
t: 时间
[s]
x:
x方向
y:
y方向
ν: 运动粘度
[m2/s]
ρ: 密度
[kg/m3]
p: 气压(实际气压和雷诺平均气压的差值)
[pa]2.将偏微分方程离散化
∂u/∂x)选用后退差分(Backward Difference),二阶偏微分(如:
∂2u/∂x2)选用中心差分(Central Difference)。
u的N-S方程式:
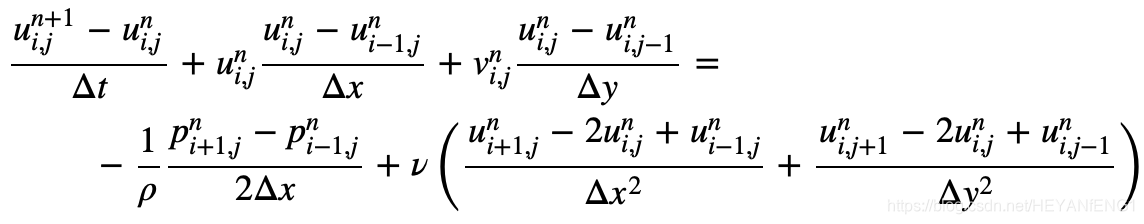
v的N-S方程式:
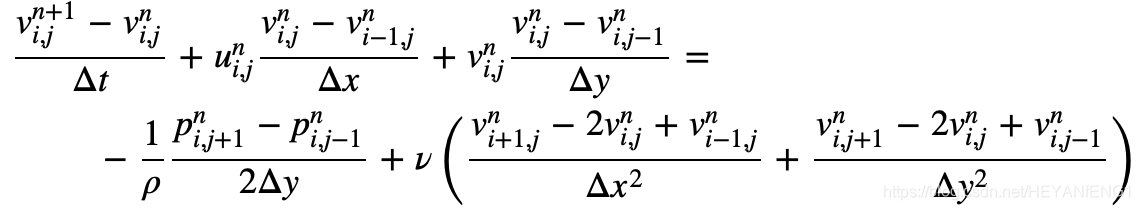
气压的泊松方程:

记号:
n:
n时点
[s]
n+1:
n+1时点(
n时点之后的一个时点)
[s]
Δt: 时间间隔
[s]
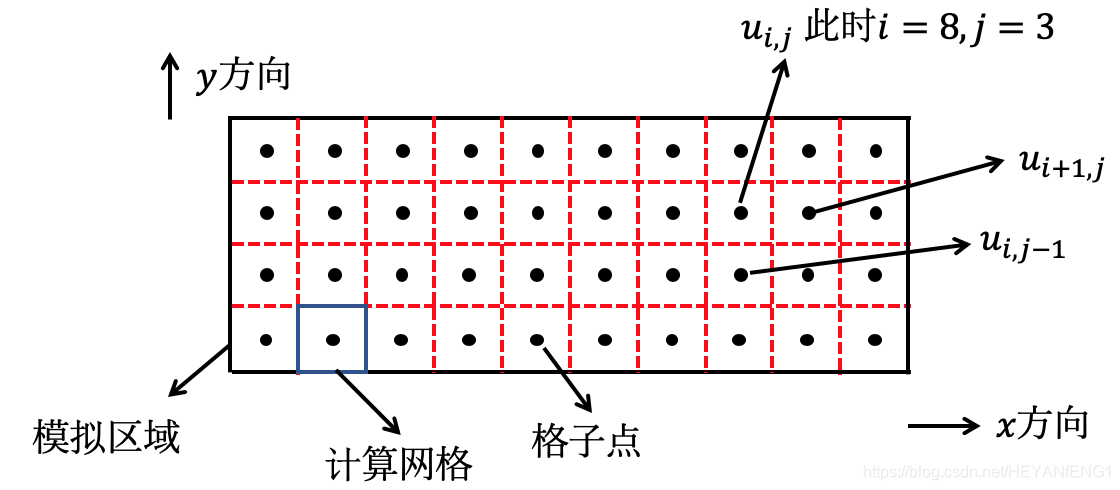
ui,j: 以模拟区域的左下角为原点的
i,j格子点处的
x方向速度
u的N-S方程式:
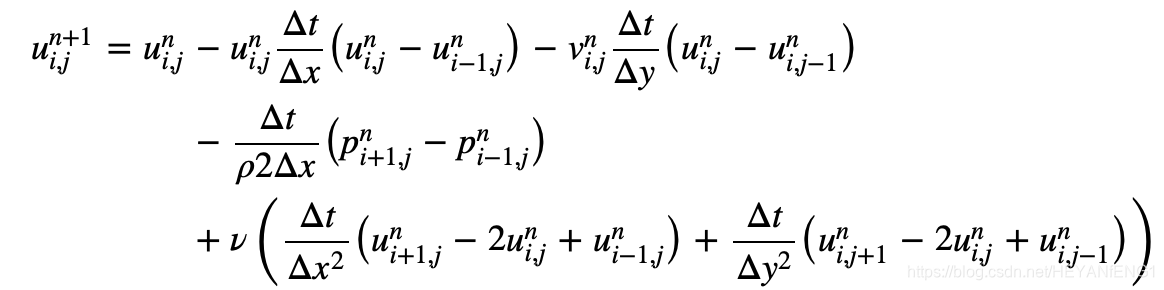
v的N-S方程式:
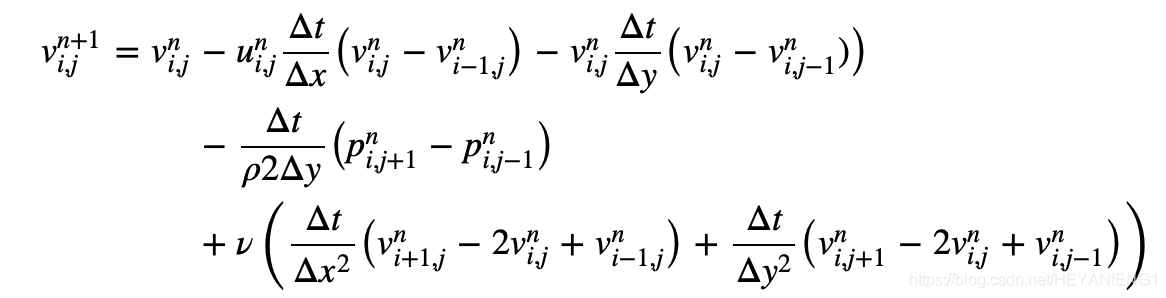
气压的泊松方程:
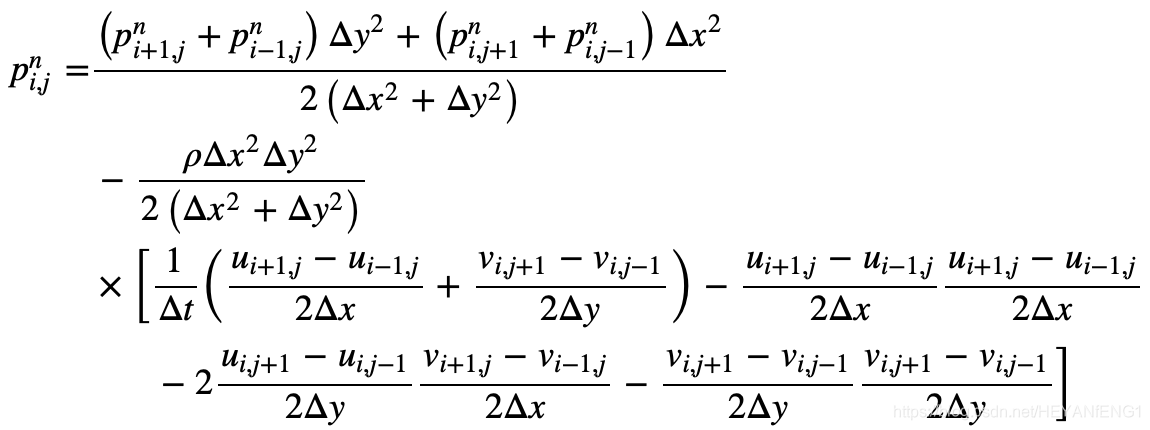
3.设置模拟条件
3.1 计算网格
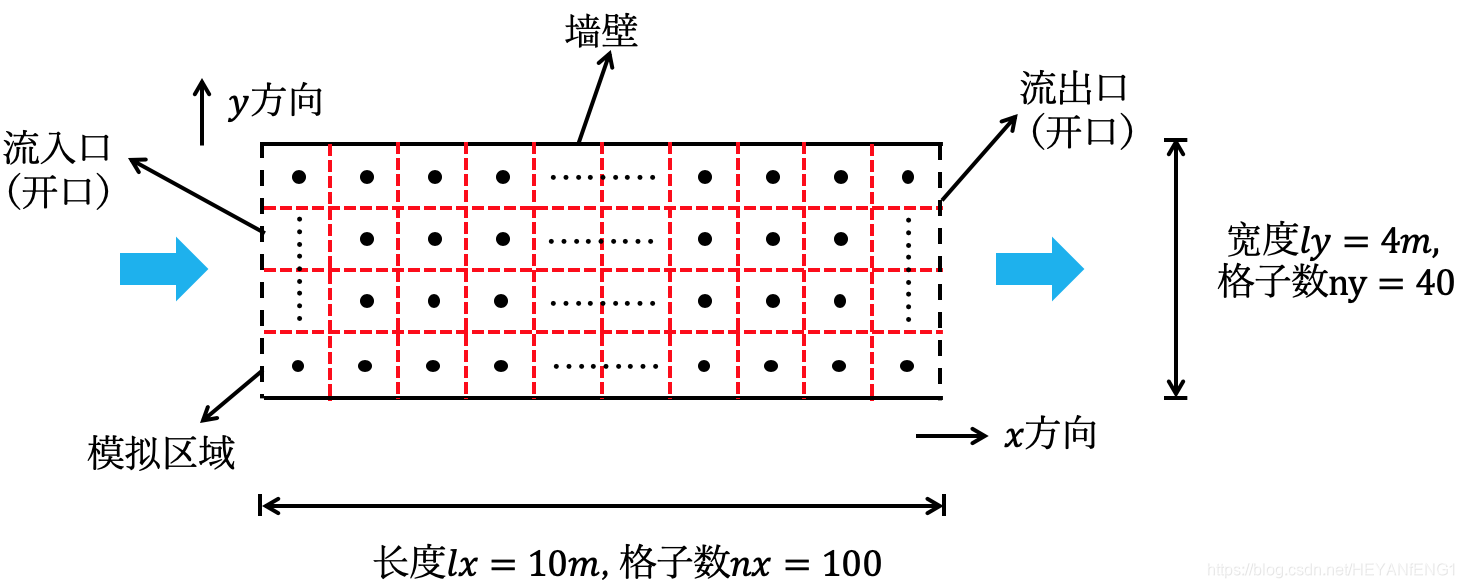
3.2 初始条件
x方向充满了
5m/s的风,
y方向充满了
3m/s的风。气压(实际气压和雷诺平均气压的差值)处处为0。3.3 边界条件

4.编写Python程序
Python程序代码见以下链接:
link
程序运行结果如下:
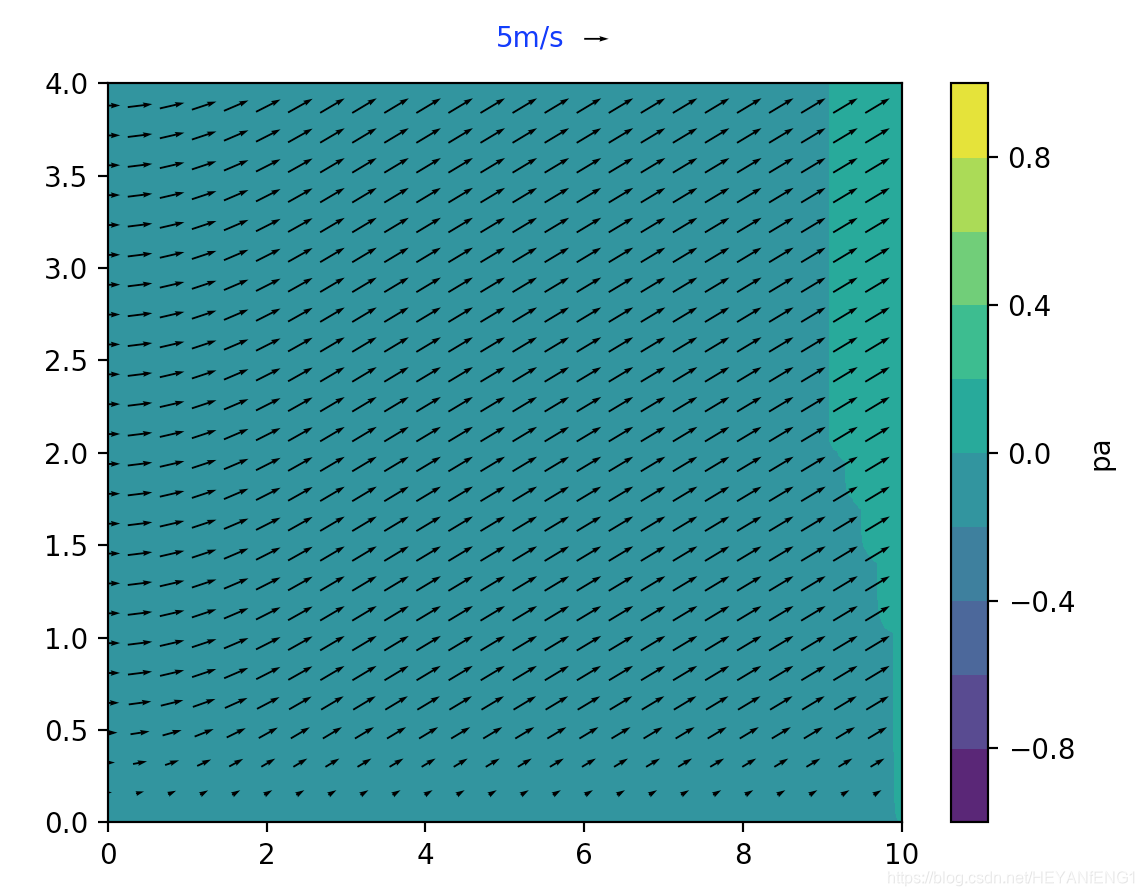
412694462@qq.com
如果您觉得本文还不错,记得点击右边打赏按钮打赏我哦~
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)