本文主讲数据库的 规范化理论，欢迎阅读~

前言

逻辑设计（即表结构的设计）
针对具体问题，构造数据模式
工具：关系数据库的规范化理论
（总结起来就是：规范化理论就是数据库中用来设计表的工具）

关系模式由五部分组成，是一个五元组：R(U, D, DOM, F)

R 是符号化的元组语义（即表名）
U 为一组属性（即属性列的集合）
D 为属性组U中的属性所来自的域
DOM 为属性到域的映射
F 为属性组U上的一组数据依赖

ps：D、DOM与模式设计关系不大，只用到三元组：R<U,F>

满足二维表每个分量必须是不可分开的数据项条件（即该表内不含有更小的表）的关系模式就属于：第一范式（1NF）
（ps：范式，Normal Form）
— — — — — — — — — — — — — — — — — —
数据依赖
是一个关系内部属性与属性之间（即列与列之间）的一种约束关系

· 通过属性间值的相等与否体现出来的数据间相互联系
· 是现实世界属性间相互联系的抽象
· 是数据内在的性质
· 是语义的体现

主要类型:

• 函数依赖（Functional Dependency，简记为FD）
• 多值依赖（Multi-Valued Dependency，简记为MVD）

函数依赖普遍存在于现实生活中：例如描述一个学生关系，可以有学号、姓名、系名等属性。

一个学号只对应一个学生，一个学生只在一个系中学习
“学号”确定后，学生姓名及所在系的值就被唯一确定。

Sname=f(Sno)，Sdept=f(Sno)
读作：Sno函数决定Sname，Sno函数决定Sdept
记作：Sno→Sname，Sno→Sdept
— — — — — — — — — — — — — — — — — —
🌟来看个例子： 现建立一个描述学校教务的数据库。涉及的对象包括： 学号（Sno），所在系（Sdept），系主任姓名（Mname），课程号（Cno），成绩（Grade）。假设学校教务的数据库模式用一个单一的关系模式Student来表示，则该关系模式的属性集合为：
U ＝ {Sno, Sdept, Mname, Cno, Grade}
现实世界的已知事实（语义，即理论基础）：

一个系有若干学生， 但一个学生只属于一个系；
一个系只有一名（正职）负责人；
一个学生可以选修多门课程，每门课程有若干学生选修；
每个学生学习每一门课程有一个成绩。

由此可得到属性组U上的一组函数依赖F： F={Sno→Sdept, Sdept→Mname, (Sno, Cno)→Grade}
此时关系模式Student(Sno, Sdept, Mname, Cno, Grade)中存在的问题有:
1）数据冗余：浪费大量的存储空间，每一个系主任的姓名重复出现
2）更新异常（Update Anomalies）：更新数据时，维护代价大：某系更换系主任后，须修改有关的每一个元组
3）插入异常（Insertion Anomalies）：如果一个系刚成立，尚无学生，则无法把这个系及其系主任存入数据库
4）删除异常（Deletion Anomalies）：如果某个系的学生全部毕业了， 则在删除该系学生信息的同时，把这个系及其系主任的信息也丢掉了

👀总结起来Student关系模式不是一个好的模式。一个“好”的模式应当不会发生插入异常、删除异常和更新异常，数据冗余应尽可能少。
分析：这些问题是由存在于模式中的某些数据依赖引起的。重点来了，可以用规范化理论改造关系模式来消除其中不合适的数据依赖
把这个单一的模式拆成三个关系模式（即拆成三个表）：

S(Sno,Sdept,Sno → Sdept);
SC(Sno,Cno,Grade,(Sno,Cno) → Grade);
DEPT(Sdept,Mname,Sdept → Mname);

现在这三个模式都不会发生插入异常、删除异常的问题，数据的冗余也得到了控制👌
好了，引入部分结束啦，下面开始详细地进行讲解~

一、函数依赖

1. 函数依赖

设R(U)是一个属性集U上的关系模式，X和Y是U的子集。
若对于R(U)的任意一个可能的关系r，r 中不可能存在：两个元组在X上的属性值相等，而在Y上的属性值不等 （有点绕口，，可理解为两个元组在X上的属性值相等，则在Y上的属性值也一定相等）
则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。
🌟看例子加深理解： Student(Sno, Sname, Ssex, Sage, Sdept), 假设不允许重名，则有：
（附上Student表）

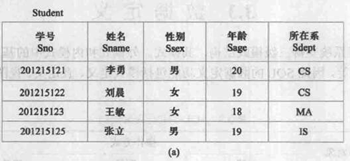
（ps：若X→Y，并且Y→X, 则记为X←→Y。若Y不函数依赖于X, 则记为X
$notrightarrow$

​→Y。）
Sno → Ssex，Sno → Sage，Sno → Sdept，
Sno ←→ Sname
Sname → Ssex，Sname → Sage，Sname → Sdept
但Ssex
$notrightarrow$

​→Sage, Ssex
$notrightarrow$

​→Sdept

2. 平凡函数依赖与非平凡函数依赖

X→Y，但Y⊈X则称X→Y是非平凡的函数依赖。
X→Y，但Y⊆X 则称X→Y是平凡的函数依赖。
即，X能函数确定Y，若Y是X的子集，则为平凡函数依赖，若Y不是X的子集则为非平凡的函数依赖。根据刚刚的定义来理解，两个元组在X上的属性值相等，那么它的子集里这两个元组的属性值也必定是相等的吖，所以平凡函数依赖都是必然成立的，我们一般讨论的是非平凡函数依赖。

👀平凡函数依赖都是必然成立的，不反映新的语义。
若不特别声明， 我们总是讨论非平凡函数依赖。
— — — — — — — — — — — — — — — — — —
若X→Y，则X称为这个函数依赖的决定因素
若X→Y，Y→X，则记作X←→Y。
若Y不函数依赖于X，则记作X
$notrightarrow$

​→Y

3. 完全函数依赖与部分函数依赖

在R(U)中，如果X→Y，并且对于X的任何一个真子集X’, 都有 X’
$notrightarrow$

​→Y, 则称Y对X完全函数依赖，记作
$X overset F rightarrow Y$

X→FY 。（即只有X自己能函数确定Y，它的任意一个子集都不能函数确定Y）
若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作
$X overset P rightarrow Y$

X→PY
🌟看例子加深理解： 在关系SC(Sno, Cno, Grade)中，有：
Sno
$notrightarrow$

​→Grade，Cno
$notrightarrow$

​→Grade，
因此：(Sno, Cno)
$overset F rightarrow$

→FGrade
(Sno, Cno)
$overset P rightarrow$

→PSno（因为Sno可以由(Sno, Cno)的子集Sno函数确定）
(Sno, Cno)
$overset P rightarrow$

→PCno（同理Cno可以由(Sno, Cno)的子集Cno函数确定）

4. 传递函数依赖

在R(U)中，如果X→Y(Y⊈X)，Y
$notrightarrow$

​→X，Y→Z，Z⊈Y, 则称Z对X传递函数依赖(transitive functional dependency)。记为：X → Z
（ps: 如果Y→X, 即X←→Y，则Z直接依赖于X，而不是传递函数依赖）

🌟看例子加深理解： 在关系Std(Sno, Sdept, Mname)中，有：
Sno → Sdept，Sdept → Mname，
所以Mname传递函数依赖于Sno

二、码

设K为R<U,F>中的属性或属性组合。
若K
$overset F rightarrow$

→FU（U完全函数依赖于K），则K称为R的一个候选码(Candidate Key)。（即K的任意真子集都不是候选码，K的任意真子集都不能函数确定U）
如果U部分函数依赖于K，即K
$overset P rightarrow$

→PU,则K称为超码 ，候选码是最小的超码。
若关系模式R有多个候选码，则选定其中的一个做为主码(Primary key)（根据实际情况，理论基础选择合适的主码）
（ps：候选码可简称为码，后面的文章内容中也会多次使用简称~）
— — — — — — — — — — — — — — — — — —
主属性与非主属性
包含在任何一个候选码中的属性 ，称为主属性
不包含在任何码中的属性称为非主属性

如果整个属性组是码，则称为全码（All-key）（即需要知道整个属性组才能唯一确定一个元组时，该码即整个属性组，成为全码）
🌟看例子加深理解：
S(Sno, Sdept, Sage)，单个属性Sno是码
SC(Sno, Cno, Grade)中，(Sno, Cno)是码

🌟看例子加深理解： R(P,W,A)，P：演奏者 W：作品 A：听众

一个演奏者可以演奏多个作品
某一作品可被多个演奏者演奏
听众可以欣赏不同演奏者的不同作品

所以需要整个属性组才能确定一个元组，码为(P,W,A)，即全码（All-Key）
— — — — — — — — — — — — — — — — — —
外码：
关系模式 R中属性或属性组X 并非 R的码，但 X 是另一个关系模式的码，则称 X 是R 的外部码（Foreign key）也称外码。（即R中的X是引用了另一个关系中的码作为外码约束，但X并不是R本身自己的码）
🌟看例子加深理解：
SC(Sno,Cno,Grade)中，Sno不是码
Sno是 S(Sno,Sdept,Sage)的码，则Sno是SC的外码
（ps：即SC表中的Sno不是SC的码，它是从S表引用过来的，Sno是S表的码，所以称Sno为SC的外码，SC和S之间具有外码约束，即参照完整性约束）

主码与外码一起提供了表示关系间联系的手段

三、范式（NF）

范式是符合某一种级别的关系模式的集合（即表的集合，因为这里不涉及表内的具体数据，所以这里研究的主要是表的结构，或者说表的属性列名之间的联系）
可分为：

第一范式(1NF)
第二范式(2NF)
第三范式(3NF)
BC范式(BCNF)
第四范式(4NF)
第五范式(5NF)

各种范式之间存在联系：1NF
$supset$

⊃ 2NF
$supset$

⊃ 3NF
$supset$

⊃ BCNF
$supset$

⊃ 4NF
$supset$

⊃ 5NF
某一关系模式R为第n范式，可简记为R∈nNF
一个低一级范式的关系模式，通过模式分解（可理解为之前提到的拆）可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化

第一范式在一开始前言部分有提到啦，第一范式很容易满足，只要是一个满足二维表每个分量必须是不可分开的数据项条件（即该表内不含有更小的表）的关系模式（表）就属于第一范式（1NF）~

第二范式（2NF）

若关系模式R∈1NF，并且每一个非主属性（不包含在任何码中的属性）都完全函数依赖于任何一个候选码，则R∈2NF。（总结一下就是2NF中非主属性和码之间不存在部分函数依赖，干掉部分函数依赖）

🌟来看例子： S-L-C(Sno,Sdept,Sloc,Cno,Grade)， Sloc为学生的住处，并且每个系的学生住在同一个地方。S-L-C的码为(Sno,Cno)。
函数依赖有：

(Sno,Cno)
$overset F rightarrow$

→FGrade
Sno→Sdept, (Sno,Cno)
$overset P rightarrow$

→PSdept
Sno→Sloc, (Sno,Cno)
$overset P rightarrow$

→PSloc
Sdept→Sloc

由表达式和图中均可看出非主属性Sdept、Sloc并不完全依赖于码，所以关系模式S-L-C不属于2NF。
— — — — — — — — — — — — — — — — — —
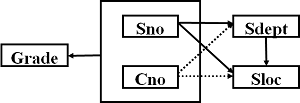
✍一个关系模式不属于2NF，会产生以下问题：
插入异常：如果插入一个新学生，但该生未选课，即该生无Cno，由于插入元组时，必须给定码值，因此插入失败。
删除异常：如果S4只选了一门课C3，现在他不再选这门课，则删除C3后，整个元组的其他信息也被删除了。
修改复杂：如果一个学生选了多门课，则Sdept，Sloc被存储了多次。如果该生转系，则需要修改所有相关的Sdept和Sloc，造成修改的复杂化。
分析：
出现的原因：例子中有两类非主属性：一类如Grade，它对码完全函数依赖；另一类如Sdept、Sloc，它们对码不是完全函数依赖
解决方法：可用投影分解把关系模式S-L-C分解成两个关系模式

SC(Sno,Cno,Grade)
S-L(Sno,Sdept,Sloc)

SC的码为(Sno,Cno)，SL的码为Sno，这样使得非主属性对码都是完全函数依赖了，即满足第二范式（2NF）了~

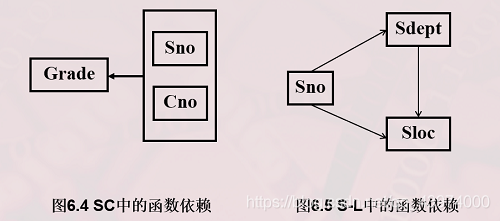
第三范式（3NF）

设关系模式R<U,F>∈1NF,若R中不存在这样的码X、属性组Y及非主属性Z（Z ⊇ Y）, 使得X→Y，Y→Z成立，Y
$notrightarrow$

​→X不成立，则称R<U,F> ∈ 3NF。（总结一下就是3NF中非主属性和码之间不存在传递函数依赖，干掉传递函数依赖）
🌟拿刚才的例子来示范：
SC没有传递依赖，因此SC ∈ 3NF
S-L中Sno →Sdept( Sdept
$notrightarrow$

​→Sno), Sdept→Sloc，可得Sno
$overset {传递} rightarrow$

→传递Sloc。
解决的办法是将S-L分解成
S-D(Sno,Sdept)∈ 3NF
D-L(Sdept,Sloc)∈ 3NF

BCNF

通常认为BCNF（Boycee Codd Normal Form）是修正的第三范式，因为其强度高于3NF，又低于4NF，有时也称为扩充的第三范式。
定义：
设关系模式R<U,F>∈1NF，若X →Y且Y ⊆ X（非平凡函数依赖）时X必含有码，则R<U,F>∈BCNF。换句话说，在关系模式R<U,F>中，如果每一个决定属性集（这里即→左边的决定因素X）都包含候选码，则R∈BCNF。

🌟来看例子： 考察关系模式C(Cno,Cname,Pcno)

C只有一个码Cno，非主属性：Canme，Pcno
没有非主属性对Cno部分依赖或传递依赖，所以C∈3NF。
C中Cno是唯一的决定因素，同时Cno是码，所以C∈BCNF。

🌟Another one： 关系模式S(Sno,Sname,Sdept,Sage)，假定Sname具有唯一性

S有两个候选码：Sno，Sname，非主属性：Sdept，Sage
非主属性不存在对码的传递依赖和部分依赖，所以S∈3NF。
S中决定因素Sno，Sname都包含码，所以S也属于BCNF。

🌟Another one： 关系模式SJP(S,J,P)中，S是学生，J表示课程，P表示名次。每一个学生选修每门课程的成绩有一定的名次，每门课程中每一名次只有一个学生（即没有并列名次）。

由语义可得到函数依赖： (S,J)→P；(J,P)→S
候选码：(S,J)，(J,P)。没有非主属性。
连非主属性都莫得，所以没有非主属性对码传递依赖或部分依赖，所SJP∈3NF。
除(S,J)与(J,P)以外没有其他决定因素，它俩都是候选码，所以SJP∈BCNF。

🌟Another one： 关系模式STJ(S,T,J)中，S表示学生，T表示教师，J表示课程。每一教师只教一门课。每门课有若干教师，某一学生选定某门课，就对应一个固定的教师。

由语义可得到函数依赖：(S,J)→T；(S,T)→J；T→J
候选码：（S,J）,（S,T），没有非主属性
没有非主属性对码传递依赖或部分依赖，STJ ∈ 3NF。
因为T是决定因素，而T不包含码，所以STJ
$notin$

∈/​BCNF。

非BCNF的关系模式也可以通过分解成为BCNF：例如STJ可分解为ST(S,T)与TJ(T,J)，它们都是BCNF。

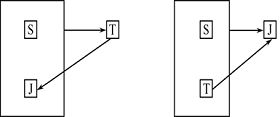
多值依赖

介绍第四范式前需要先了解多值依赖，所以咱们先来康康多值依赖叭~
🌟先引入一个例子： 设学校中某一门课程由多个教师讲授，他们使用相同的一套参考书。每个教员可以讲授多门课程，每种参考书可以供多门课程使用。
关系模式Teaching(C,T,B)，课程C，教师T，参考书B。

首先来康非规范化关系表（适合于我们人看的~）：

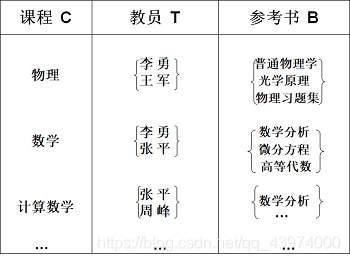
可见表中出现了一对多的关系，不是规范的二维表结构，下面才是规范化的二维表 Teaching ：

定义：
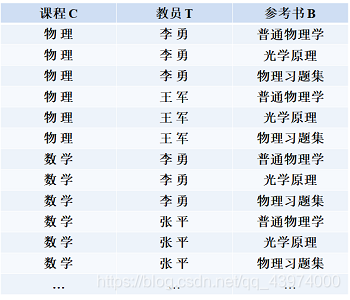
设R(U)是属性集U上的一个关系模式。X,Y,Z是U的子集，并且Z=U-X-Y。关系模式R(U)中多值依赖X→→Y成立，当且仅当对R(U)的任一关系r，给定的一对(X,Z)值，有一组Y的值，这组值仅仅决定于X值而与Z值无关。
🌟加深理解： 对于刚刚的Teaching（C, T, B）
Teaching具有唯一候选码(C,T,B)， 即全码，所以Teaching∈BCNF。
对于课程C的每一个值，教师T都有一组值与之对应，而不论参考书B取何值，因此T多值依赖于C，即C→→T。 （例如上图中的数学课对应老师李勇和张平，物理课对应李勇和王军，无论用的是哪本参考书，任意一门课程都有一组老师与之对应）

平凡多值依赖和非平凡的多值依赖：
对于刚刚的定义，若X→→Y（Y多值依赖于X），而Z＝Ф（Z为空），则称X→→Y为平凡的多值依赖。
否则称X→→Y为非平凡的多值依赖。（我们还是以研究非平凡的为主~）
🌟来看例子： 关系模式WSC(W,S,C)中，W表示仓库，S 表示保管员，C 表示商品。假设每个仓库有若干个保管员，有若干种商品。每个保管员保管所在仓库的所有商品，每种商品被所有保管员保管。
（如下图，例如W1仓库，有两个保管员S1和S2，W1中有三种商品C1、C2、C3，S1和S2都要保管W1中的所有商品，即这三种商品被W1中的S1和S2保管，可发现商品和保管员是完全对称的）

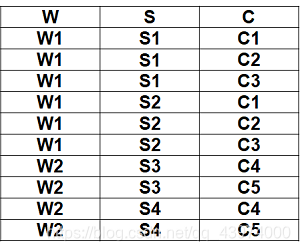
所以按照语义对于W的每一个值W_i，S有一个完整的集合与之对应而无论C取何值（这里和刚刚介绍的课程，老师，参考书的那个表的对应关系如出一辙哈）。所以W→→S。
又以为C与S的完全对称性，所以有W→→C成立。

第四范式（4NF）

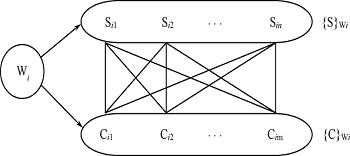
关系模式R<U,F>∈1NF，如果对于R的每个非平凡多值依赖X→→Y（Y ⊈ X），X都含有码，则R<U,F>∈4NF。
（ps：如果一个关系模式是4NF， 则必为BCNF）
🌟加深理解： 在上面的WSC关系模式中，W →→S, W→→C，他们都是非平凡多值依赖。但是W不是码，关系模式WSC的码是(W,S,C)，即All-key全码，所以WSC
$notin$

∈/​ 4NF。
可以把WSC分解成WS(W,S)，WC(W,C)，就能得到 WS∈4NF，WC∈4NF。

四、规范化小结

规范化过程总结如下：

所以找对候选码很重要！！！以下对找候选码做一些总结：
🌟来看例1： 设关系模式 U=(A , B , C , D )，函数依赖集 F={D→ B , B → D , AD → B , AC → D}，求U的候选码：

首先使用“笨办法”一个一个找，先从一个候选码找起，根据函数依赖集F可以判断一个的候选码没有，所以找两个的作为候选码，AB尝试不行，AC尝试成功~所以AC是候选码

但是这个方法在简单问题还可以使用，题目难了之后比较乏力，所以这里要介绍的方法是：闭包！，不过不用担心，这里只是运用一部分知识能求解候选码即可，并不深入研究哈~
— — — — — — — — — — — — — — — — — — — — — —
闭包（记作X^＋） 就是由一个属性直接或间接推导出的所有属性的集合。
例如：f={a->b，b->c，a->d，e->f}；
由a可直接得到b和d，间接得到c，所以a的闭包就是{a，b，c，d}
👀对于给定的关系R（A1，A2，…An）和函数依赖集F，可将其属性分为4类：

L类：仅出现在函数依赖左部的属性。
R 类：仅出现在函数依赖右部的属性。
N 类：在函数依赖左右两边均未出现的属性。
LR类：在函数依赖左右两边均出现的属性。

定理一： 对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，则X必为关系R的任一候选码的成员。
推论： 对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类属性，且X⁺（X的闭包）包含了R的全部属性；则X必为R的唯一候选码
🌟例： 设有关系模式R（A，B，C，D），其函数依赖集F={D→B，B →D，AD →B，AC →D}，求R的所有候选码：
观察F发现，A，C两属性是L类属性，所以AC必是R的候选码成员，又因为（AC）⁺= {A, B, C, D}，包含了R的全部属性，所以AC是R的唯一候选码。

定理二： 对于给定的关系模式R及其函数依赖集F，若X（X∈R）是R类属性，则X不在任何候选码中。

定理三： 对于给定的关系模式R及其函数依赖集F，若X（X∈R）是N类属性，则X必包含在R的任一候选码中。

推论： 对于给定的关系模式R及其函数依赖集F，若X（X∈R）是L类和N类组成的属性集，且X⁺包含了R的全部属性；则X是R的唯一候选码。（这里和刚刚的定理一对比着记忆~）
— — — — — — — — — — — — — — — — — — — — — —
了解了用闭包来求候选码，现在🌟回到例1中： 设关系模式 U=(A , B , C , D )，函数依赖集 F={D→ B , B → D , AD → B , AC → D}，求U的候选码：

(1) L=(A , C )，即L类属性有A，C； R=空，即无R类属性；LR=(B , D )，N=空;
(2) L ∪ N=(A , C )，因为(AC)⁺=ACBD=U, 所以AC 是唯一候选码

— — — — — — — — — — — — — — — — — — — — — —
🌟来看例2： R<U,F>,U=(A,B,C,D,E,G)，F={AB->C,CD->E,E->A，A->G}，求候选码：

(1) L=(B,D), R=(G), LR=(A,C,E ), N=空;
(2) L ∪ N=(B,D) BD⁺=BD;
(3)ABD：AB–>C,CD–>E,A–>G，所以ABD⁺= ABDCEG=U
BDC：CD–>E,E–>A,A–> G，所以BDC⁺= BDCEAG=U
BDE：E–>A,A–>G,AB–>C，所以BDE⁺= BDEAGC=U
所以候选码有3个分别是ABD、BCD和BDE

— — — — — — — — — — — — — — — — — — — — — —
🌟来看例3： 设关系模式 U=(A , B , C , D , E , F )，函数依赖集F={A→ BC , BC → A , BCD → EF , E → C}，求 R 的候选码：

(1) L=(D), R=(F ), LR=(A , B , C , E ), N=空;
(2) L∪N=(D) D⁺=D;
(3)因为 DA⁺=DABCEF=U, DB⁺=DB DC⁺=DC, DE⁺=DEC, 所以 DA 是候选码;
(4)因为 DBC⁺=DBCAEF=U, DBE⁺=DBECAF=U, DCE⁺=DCE, 所以 DBC、DBE也是候选码;
综上所述，U 的候选码有 DA 、 DBC 、 DBE

🔥不能说规范化程度越高的关系模式就越好。
必须对现实世界的实际情况和用户应用需求作进一步分析，确定一个合适的、能够反映现实世界的模式，所以说上面的规范化步骤可以在其中任何一步终止~

五、课后习题

习题来源链接：【2019-2020春学期】数据库作业15：第六章： 关系数据理论
嘻嘻，因为这部分习题几乎不涉及写代码，我就直接手写上传照片啦~





嘻嘻，为了尽量少占空间，我把照片都旋转了90度，如有不适还请体谅~

那，数据库的规范化总算是整理完啦，感谢阅读~😊 最后的习题可能有影响到整体的观看体验（我的字真的写的一言难尽啊😅，一定要好好练字~） 对了，如文中有不恰当的地方，望提出指正~

• 相关推荐：【吐血整理】数据库的完整性
• 安利一下：SQL Server 创建登录名和用户名【详细介绍】