(本文主要介绍卷积神经网络工作原理以及用卷积神经网络处理mnist数据集,并附代码) 效果如下: 和基础神经网络一样,CNN也有由输入层——隐藏层——输出层构成的。 和基础神经网络不一样的是,CNN的输入数据是二维的,可以直接处理数字化的图片。这个例子中输入数据是多个28×28×1的图片。这里的三个数值分别对应图片的长宽,以及‘通道’。这个通道,本次例子是黑白图片,所以只有一个通道,而常规彩色图是有三个通道(RGB通道),即要把图片理解成三维的,而输入数据是很多个图片,所以输入数据要理解成四维。(这里比较难理解,看了后面的可能会帮助理解) 隐藏层是CNN最关键也是最难理解的地方,这一层的操作包括了卷积操作,激活操作和池化操作,其目的是对这些图片像素信息进行特征提取。我们先来聊卷积操作。 这就是一次卷积。 之后进行ReLu操作,再就是池化层。 最后在将隐藏层操作组合一下,每一个隐藏层做的是,卷积—激活—池化。 这就是隐藏层所做的工作。 首先我们做好准备工作: 然后我们用keras导入数据,并将数据进行归一化操作: 然后我们再来固定输入shape并且定义第一个filter和偏置: 下面我们将输入数据变成28×28的形式: 之后我们通过softmax激活函数将它映成一个十维度概率向量: 下面我们来进行反向传播: 这些都定义好了,我们就可以开始迭代了。 在开始迭代之前,要先说明一些事项。 这里给大家提供一个逐个batch迭代的模板。(也正是因为这个原因,再加上解释之前的编码操作,我才没有用input_data进行mnist数据下载,因为这样做直接什么都做好了,也就不需要这些代码的操作,不利于小伙伴们理解。) 下面进行tensorflow的初始化操作(这个没什么可说的,用了tensorflow这个框架就得按照人家的规定来): 正式开始迭代,并定义一些打印某些数值的规则: 用mnist数据集训练好了手写数字识别后,加上定位方法,就可以做手写邮编数字识别了。 (图片大多来自唐宇迪神经网络PPT) (说明一下我只是个大四在读学生,在自学深度学习,期间遇到很多问题,通过各种资料解开了疑问。写这篇博客的目的是加深对理论的理解,同时也希望能给和我一样存在疑问的初学者一些参考。所以请各位大佬在看到错误的时候指出来,不胜感激!)
先给大家看一下成果:
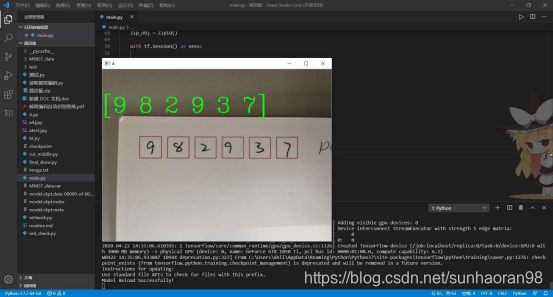
机器精准的识别了邮编上的手写数字。我们今天要聊的就是如何用CNN训练mnist手写数字数据集。
话不多说,先上代码,之后再聊卷积神经网络的工作原理。(这段代码并非追求简洁,而是定义了很多函数,方便下面讲解CNN的工作原理)import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib.cm as cm import tensorflow as tf LEARNING_RATE = 1e-4 TRAINING_ITERATIONS = 2500 DROPOUT = 0.5 BATCH_SIZE = 50 VALIDATION_SIZE = 2000 IMAGINE_TO_DISPLAY = 10 from tensorflow import keras (x_train,y_train),(x_test,y_test) = keras.datasets.mnist.load_data() x_train = np.multiply(x_train,1.0/255.0).astype(np.float32) x_test = np.multiply(x_test,1.0/255.0).astype(np.float32) def dense_to_one_hot(labels_dense,num_classes): num_labels = labels_dense.shape[0] index_offset = np.arange(num_labels) * num_classes labels_one_hot = np.zeros((num_labels,num_classes)) labels_one_hot.flat[index_offset + labels_dense.ravel()] = 1 return labels_one_hot y_train = dense_to_one_hot(y_train,10).astype(np.float32) y_test = dense_to_one_hot(y_test,10).astype(np.float32) def weight_variable(shape): initial = tf.truncated_normal(shape,stddev=0.1) return tf.Variable(initial) def bias_variable(shape): initial = tf.constant(0.1,shape=shape) return tf.Variable(initial) def conv2d(x,W): return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME') def max_pool_2x2(x): return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME') x_train = x_train.reshape([-1,784]) x_test = x_test.reshape([-1,784]) # input and output x = tf.placeholder('float', shape=[None, 784]) y_ = tf.placeholder('float', shape=[None, 10]) #第一个卷积层计算 #宽5 高5 channel为1 用多少个filter来计算,这里是32 W_conv1 = weight_variable([5, 5, 1, 32]) #执行卷积后得到了32个图,所以需要32个偏置 b_conv1 = bias_variable([32]) # (40000,784) => (40000,28,28,1) image = tf.reshape(x, [-1,28 , 28,1]) #print (image.get_shape()) # =>(40000,28,28,1) h_conv1 = tf.nn.relu(conv2d(image, W_conv1) + b_conv1) #print (h_conv1.get_shape()) # => (40000, 28, 28, 32) h_pool1 = max_pool_2x2(h_conv1) W_conv2 = weight_variable([5, 5, 32, 64]) b_conv2 = bias_variable([64]) h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2) #print (h_conv2.get_shape()) # => (40000, 14,14, 64) h_pool2 = max_pool_2x2(h_conv2) W_fc1 = weight_variable([7 * 7 * 64, 1024]) b_fc1 = bias_variable([1024]) # (40000, 7, 7, 64) => (40000, 3136) h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64]) h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1) keep_prob = tf.placeholder('float') h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob) W_fc2 = weight_variable([1024, 10]) b_fc2 = bias_variable([10]) y = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2) #print (y.get_shape()) # => (40000, 10) # cost function cross_entropy = -tf.reduce_sum(y_*tf.log(y)) # optimisation function train_step = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(cross_entropy) # evaluation correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1)) accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float')) # prediction function #[0.1, 0.9, 0.2, 0.1, 0.1 0.3, 0.5, 0.1, 0.2, 0.3] => 1 epochs_completed = 0 index_in_epoch = 0 num_examples = x_train.shape[0] # serve data by batches def next_batch(batch_size): global x_train global y_train global index_in_epoch global epochs_completed start = index_in_epoch index_in_epoch += batch_size # when all trainig data have been already used, it is reorder randomly if index_in_epoch > num_examples: # finished epoch epochs_completed += 1 # shuffle the data perm = np.arange(num_examples) np.random.shuffle(perm) x_train = x_train[perm] y_train = y_train[perm] # start next epoch start = 0 index_in_epoch = batch_size assert batch_size <= num_examples end = index_in_epoch return x_train[start:end], y_train[start:end] # start TensorFlow session init = tf.initialize_all_variables() sess = tf.InteractiveSession() sess.run(init) # visualisation variables train_accuracies = [] validation_accuracies = [] x_range = [] display_step=1 for i in range(TRAINING_ITERATIONS): #get new batch batch_xs, batch_ys = next_batch(BATCH_SIZE) # check progress on every 1st,2nd,...,10th,20th,...,100th... step if i%display_step == 0 or (i+1) == TRAINING_ITERATIONS: train_accuracy = accuracy.eval(feed_dict={x: batch_xs, y_: batch_ys, keep_prob: 1.0}) if(VALIDATION_SIZE): validation_accuracy = accuracy.eval(feed_dict={ x: x_test[0:BATCH_SIZE], y_: y_test[0:BATCH_SIZE], keep_prob: 1.0}) print('training_accuracy / validation_accuracy => %.2f / %.2f for step %d'%(train_accuracy, validation_accuracy, i)) validation_accuracies.append(validation_accuracy) else: print('training_accuracy => %.4f for step %d'%(train_accuracy, i)) train_accuracies.append(train_accuracy) x_range.append(i) # increase display_step if i%(display_step*10) == 0 and i: display_step *= 10 # train on batch sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys, keep_prob: DROPOUT})
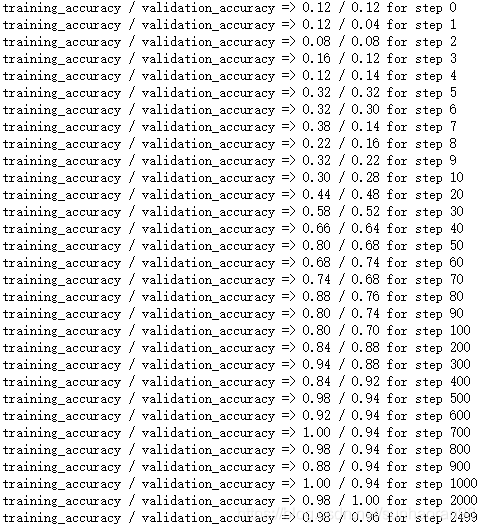
可以看出一开始迭代效果并不好,但随着迭代次数的增加,CNN甚至能做到接近1.0的分类准确率。那么,效果如此好的模型,它的工作原理是什么呢?
卷积神经网络大致是这样工作的:
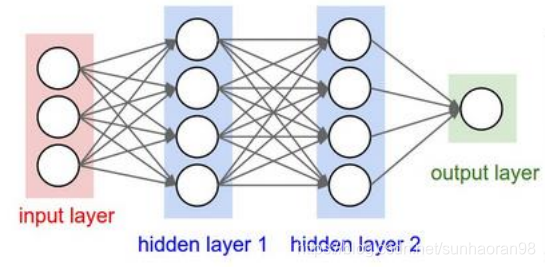
而其中隐藏层和传统神经网络不同,剖开来看,上图是这样的:
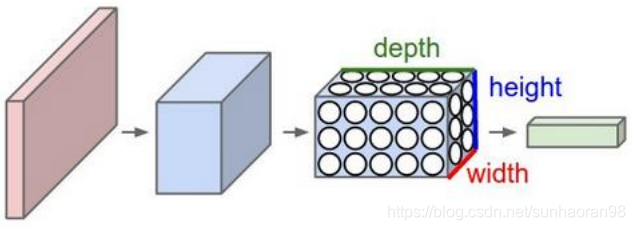
输入层
隐藏层
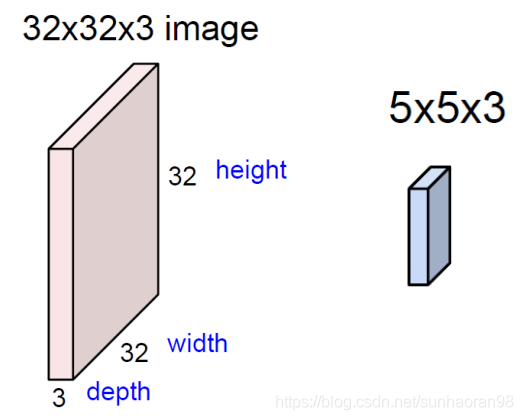
现在有一个32×32×3的图片,我们要在其中提取特征,就要借助一个叫filter(过滤器)的东西,就是后面那个5×5×3的东西,我们可以把它看成是三个5×5矩阵拼在一起,分别对输入数据的三个通道进行运算,后确定图片在一个小区域上的特征(5×5区域)。
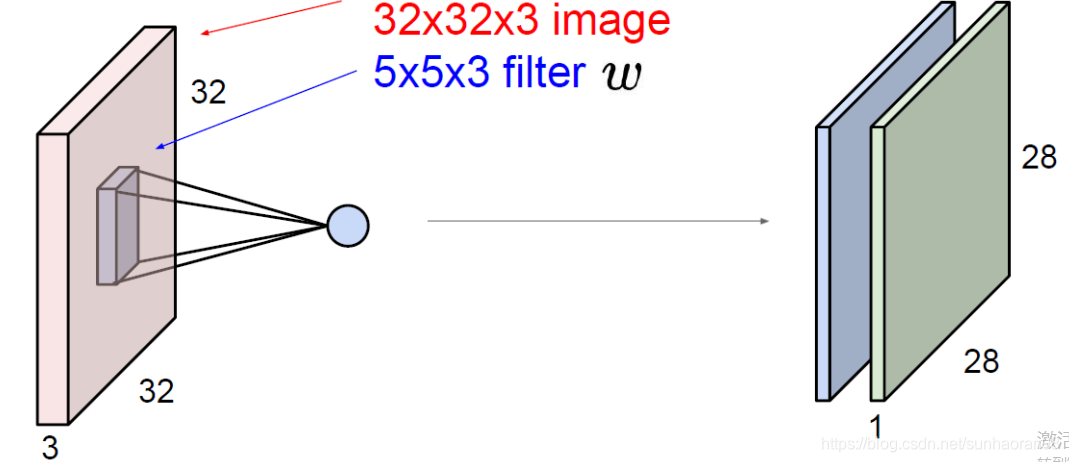
这里右边之所以是两个特征图,是因为我们用了两个filter进行特征提取(类似其他算法的多个特征提取),而提取后结果是28×28的原因我们后面会介绍。
具体的特征提取过程如下:
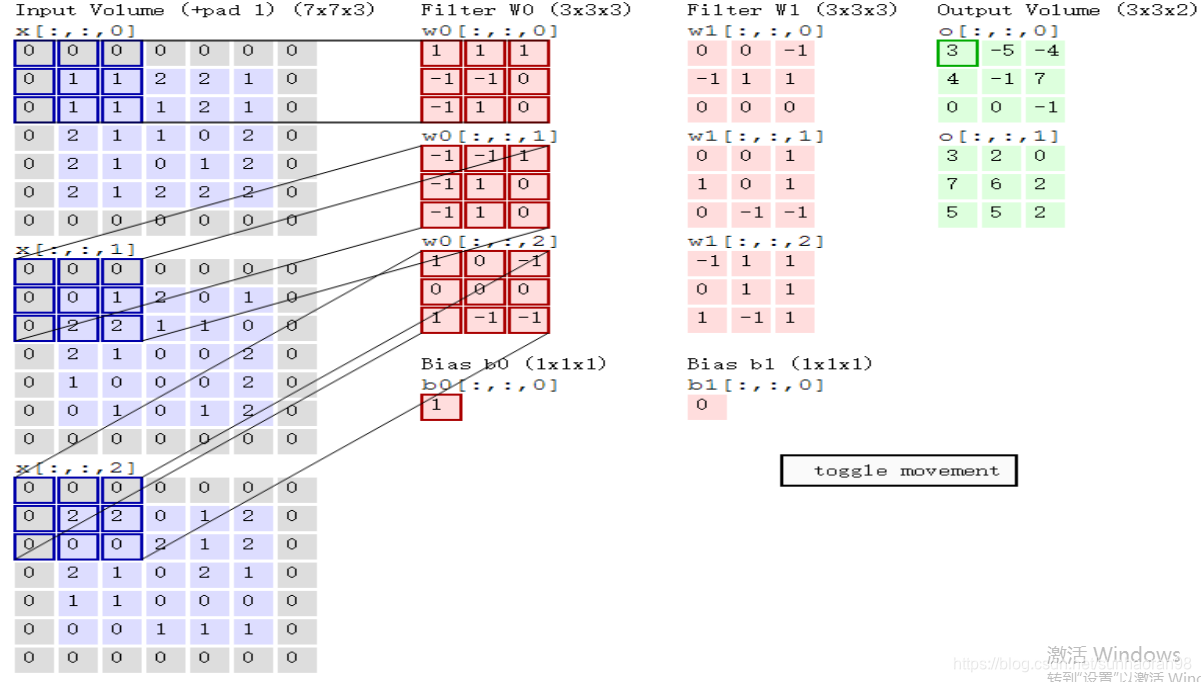
我们来解释一下这张图。左侧蓝色的矩阵是图像的三个通道,中间两个红色的矩阵是两个filter (3×3×3的),可以理解成把三个3×3的矩阵铺开,分别对左边图像的三个通道进行特征提取。
这里拿第一个filter举例:filter一次只对图像的一小块特征进行提取,即确定一个值来表示这一个小区域的特征。这里filter的三层矩阵分别对图片的三个通道进行提取操作,这个操作不是矩阵乘法,而是求内积,即对对应位置相同的各个点相乘,最后相加。
用第一个通道举例:画蓝框部分的特征(第一个3×3):0×1+0×1+0×1+0×(-1)+1×(-1)+1×0+0×(-1)+1×1+1×0 = 0
同样的,第二个通道可以算出来是2,第三个通道算出来是0
我们再把这三个特征相加,再加上下面对应的偏置项1,输出结果为3,对应绿色图中第一个数值(加了绿方框)。
再将蓝色方框进行移动,对图片第二块特征进行提取(这里滑动两步):
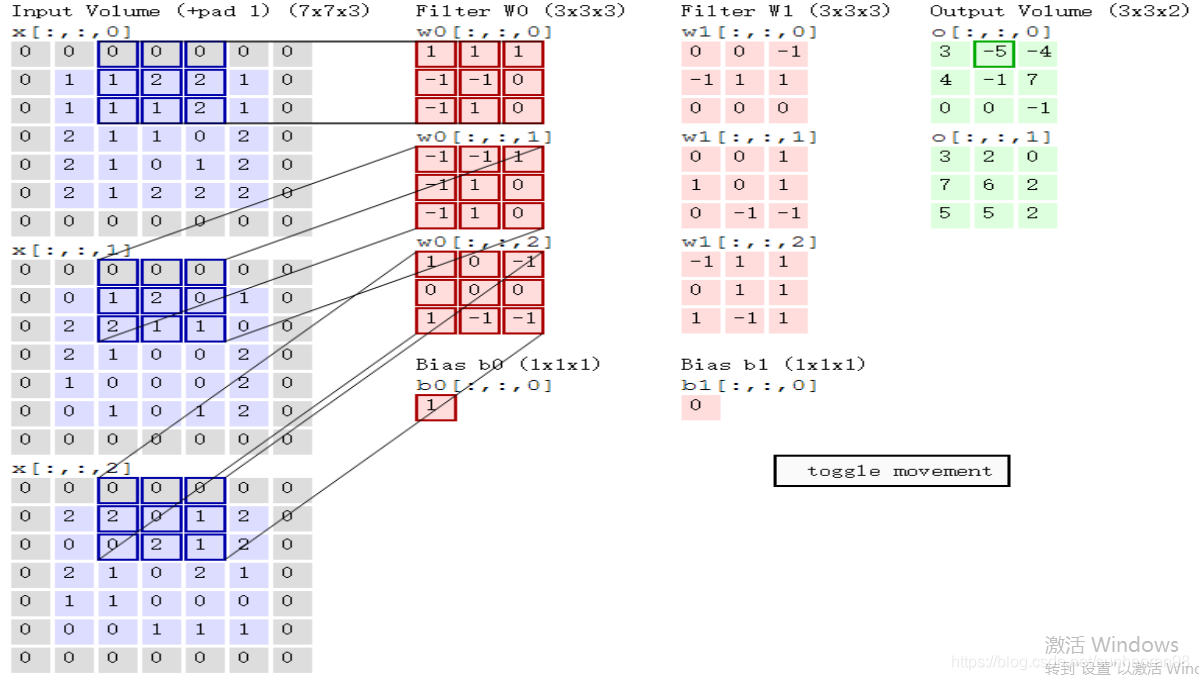
即对应绿色输出的第二个值,-5.以此类推,得到绿色框。
这里绿色框为两个filter分别对图片进行卷积操作后的结果。
上面的将32×32×3的图片提取成28×28×2的特征图是在外面加了一圈0,之后用2个5×5×3的filter进行每次滑动一步的操作得到的。滑动一次多获得一个特征,在每一行滑动了27次。
之所以在外圈加一圈0(上述举例也是这么做的),是因为在滑动过程中,边缘数据只被框住一次,而中间数据大多被框住两次以上,所以在边缘加一圈0,来让原本的边缘数据得到多一次被提取的机会。
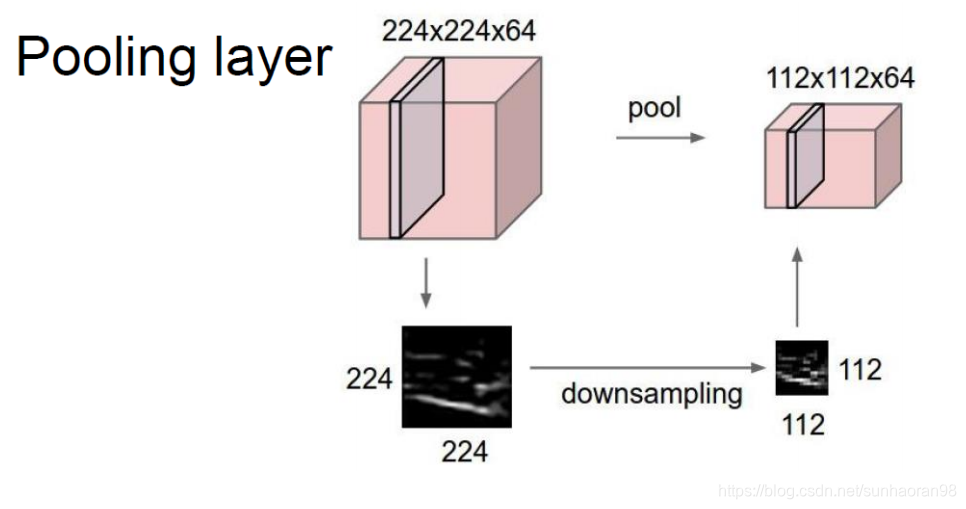
池化层操作是对卷积得到的特征进一步进行提取,一般我们采用maxpooling,即对一块区域,将其最大值作为提取的特征值。
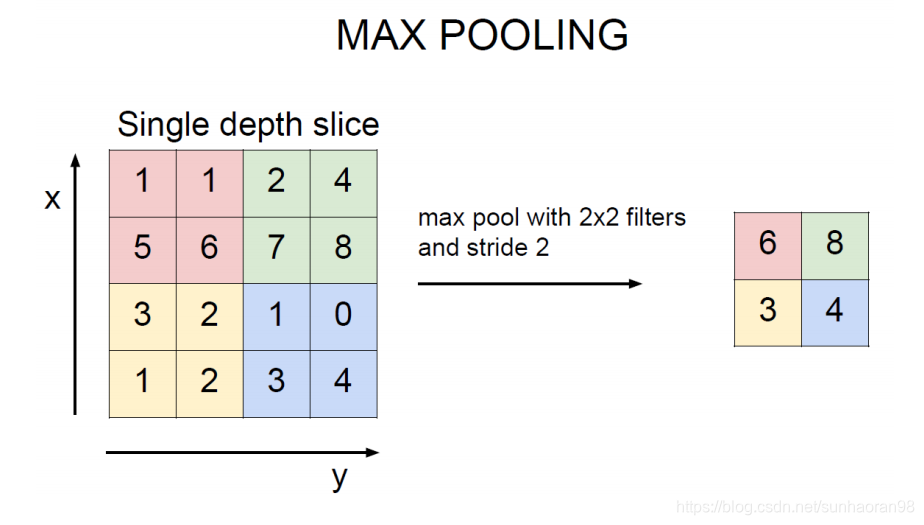
如图:红色区域最大值是6,池化操作提取出来的特征就是6,以此类推。
那么对于多个隐藏层,其步骤是:
最后输出认为该图片属于车的概率最大。
CNN的工作流程大致就是这些,下面我们来解释代码:代码详解(为了详细步骤,所以代码比一般的复杂)

里面的learningrate是学习率
trainingiterations是迭代步数
dropout是每次保留的比例
batchsize是每个batch包含的样本数
imaginetodisplay是后面效果展示用的,隔多少步展示一次。

之后我们将y(label值进行编码):
(为什么这么做可以查看我上一篇博客
https://editor.csdn.net/md/?articleId=105677771)

之后我们定义一些函数:

其中第一个函数用来固定filter的shape
第二个函数用来固定偏置项shape
第三个函数是卷积操作(2维),其中x是输入数据,W是filter,strides是滑动步长。
这里解释一下strides为什么是四维的,之前我们的图片例子中(就是很多个矩阵那个图),是一次滑动两步,其实在这里它是一个四维滑动,第一个维度是一次迭代一张图像,第二三个维度是图像的高和宽,第四个是图像的通道。(mnist数据集是黑白的只有一个通道,彩色图片有三个通道),这里表示宽高都是每次滑动一步,想改步长,就改中间两个维度。padding表示是否在周围填充一圈0.
第四个函数是池化操作,其中的strides中第二三个维度是表示对2×2区域做一个池化。(和上述例子一样)

这里我们先固定住输入数据的shape,个固定输入为784维(先拉直,后面会reshape回28×28)
这里做变换是为了方便大家理解,在每次输入的时候记得看一下输入数据是否达到卷积操作需要的shape,如果不是,那么要进行reshape。
W_conv1是第一个filter,参数表示有32个filter,b_conv1是第一个偏置。

这样数据形式就符合卷积操作需要的shape了,然后我们进行卷积池化操作:

把数据变成了一组28×28×32(32表示32个filter提取的32个特征)
之后我们进行第二轮卷积激活池化操作,再将每个图片提取好的特征reshape成一个维度。

每一次卷积或池化操作改变的数据维度代码中有解释。前面的40000大家打出来是一个‘?’,表示的是输入图片的个数,这里后面我们是输入40000个数据(也可能是60000个)
(前面把特征转换成一个维度是为了方便这一层的操作)
(关于softmax激活函数可以参考我之前的博客
https://editor.csdn.net/md/?articleId=105626726)

这样我们的前向传播就定义好了。

我们用log损失函数,train_step那行表示我们要最小化定义的cross_entropy这个损失函数,里面的参数LEARNING_RATE,是我们最开始定义的学习率,即优化步长。
(关于反向传播是如何优化的,可以去参考相关文献,理论比较复杂,本文不做介绍)
同时也定义了精度accuracy。
这里提一下,我们全连接层softmax激活函数映射出的概率向量,即为这个图片属于哪一类的概率,如映射结果为[0.1, 0.9, 0.2, 0.1, 0.1 0.3, 0.5, 0.1, 0.2, 0.3] ,那么我们就认为属于1的概率最大,为0.9,于是我们认为这个数字是1。
(从0开始,1是第二个数字)
给初次接触tensorflow编程的小伙伴们解释一下batch,batch_size,epoch的概念。
比如有10000个图片,计算机无法一次计算这么大的数据,我们一般选择128,或64个数据为一个batch,128或64就是一个batchsize。我们将10000个数据分成几个batch进行迭代,每个batch迭代完优化一次参数,所有样本迭代一遍为一个epoch(这个例子中,若选择64为batchsize,那么一个epoch就是(10000/64)取整+1 个batch,权重参数在一个epoch期间也是更新了这些次,对于剩余样本不足一个batch的情况,我们在所有样本中随机抽取补满这个batch。如果将epoch值设成10次,意味着所有样本基本上都要迭代10遍(被抽到补位的样本被迭代的次数要多一些)。
有了这个next_batch模板,就可以直接调用进行迭代了。

那么我们的效果:
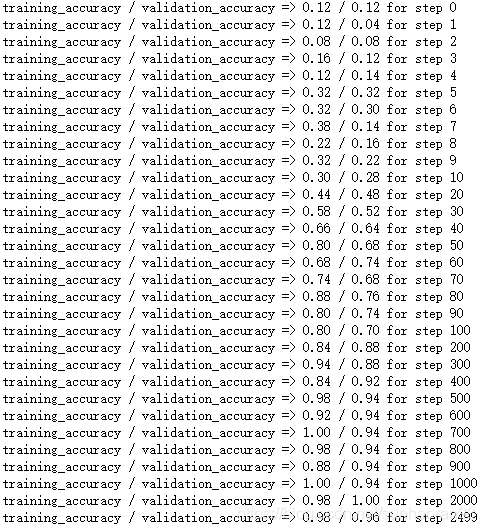
可以看出CNN的精度已经非常接近1,效果比拉直图片用传统神经网络效果要好一些。
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)