【SVM算法】{1} —— 基于最大间隔分隔数据数据结构与算法Giyn-

支持向量机模型的代价函数：

如果有一个正样本
$y=1$

y=1，其实仅仅要求
$θ^Tx$

θTx 大于等于0，就能将该样本恰当分出，这是因为如果
$θ^Tx$

θTx >0 的话，代价函数值为0；类似地，如果有一个负样本，则仅需要
$θ^Tx$

θTx<=0 就会将负例正确分离。但是，支持向量机的要求更高，不仅仅要能正确分开输入的样本，即不仅仅要求
$θ^Tx$

θTx>0，它需要的是比0值大很多，比如大于等于1，或者比0小很多，比如小于等于-1，这就相当于在支持向量机中嵌入了一个额外的安全因子，或者说安全的间距因子。

支持向量机的决策边界：

假设将常数
$C$

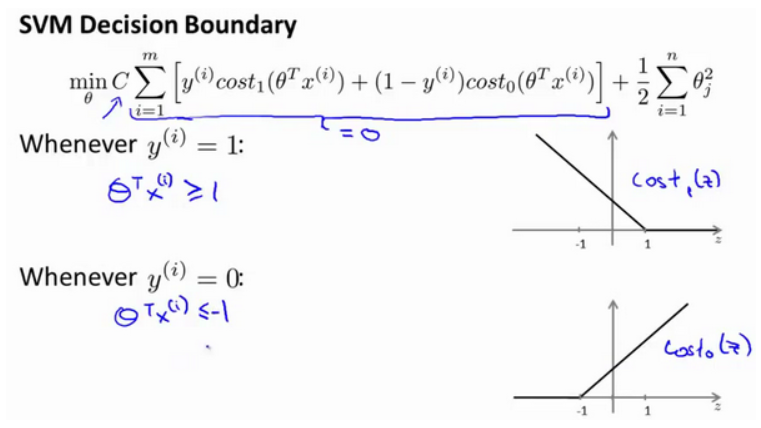
C 设为一个非常大的值，观察支持向量机会给出什么结果？

如果
$C$

C 非常大，则最小化代价函数的时候，我们将会很希望找到一个使第一项为0的最优解。

在代价项为0的情形下，将有如下约束：如果
$y^{(i)}$

y(i) = 1，
$θ^Tx^{(i)}>=1$

θTx(i)>=1 ；如果
$y^{(i)}$

y(i) = 0，
$θ^Tx^{(i)}<=-1$

θTx(i)<=−1。
这样当最小化这个关于变量
$θ$

θ 的函数的时候，你会得到一个非常有趣的决策边界：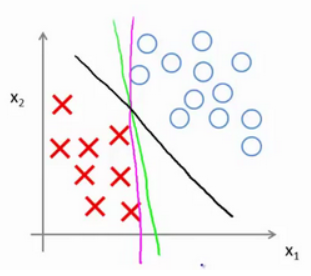

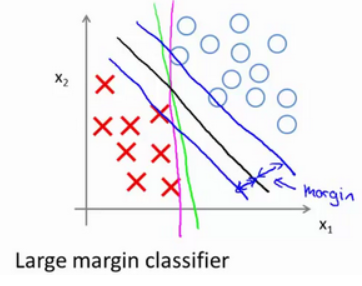
三条决策边界中，黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得更好。从数学上来讲，这条黑线有更大的距离，这个距离叫做间距(margin)。

当画出两条额外的蓝线，黑色的决策界和训练样本之间有更大的最短距离，这个距离叫做支持向量机的间距，而这是支持向量机具有鲁棒性的原因，因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器。

对代价函数的条件更严格而产生的决策边界

在让代价函数最小化的过程中，我们希望找出在
$y=1$

y=1 和
$y=0$

y=0 两种情况下都使得代价函数中左边一项尽量为零的参数。如果我们找到了这样的参数，则我们的最小化问题便转变成：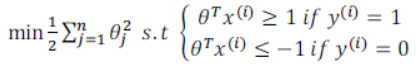

事实上，支持向量机要比上述大间距分类器体现得更成熟，尤其是当你使用大间距分类器的时候，你的学习算法会受异常点(outlier) 的影响，比如加入一个额外的正样本：

仅仅基于一个异常值，仅仅基于一个样本，就将决策界从这条黑线变到这条粉线，这实在是不明智的。

实际上应用支持向量机的时，当
$C$

C 不是非常非常大的时候，它可以忽略掉一些异常点的影响，得到更好的决策界。甚至当你的数据不是线性可分的时候，支持向量机也可以给出好的结果。

C较大时，可能会导致过拟合，高方差。
C较小时，可能会导致低拟合，高偏差。