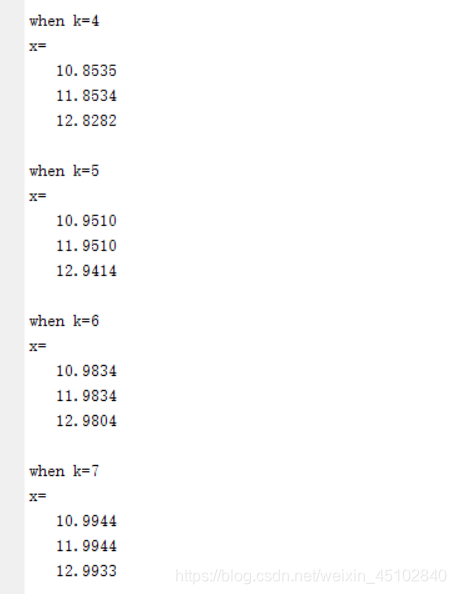
迭代法解线性方程组的基本思想是构造一串收敛到解的序列,即建立一种从已有近似解计算新的近似解的规则,有不同的计算规则得到不同的迭代法。 本文是常用的迭代法之一:Jacobi迭代法解线性方程组的matlab实现。 关于Jacobi迭代法的具体内容和算法见《数值计算方法》—丁丽娟,P65-66 书中算法如下: 程序中所用算法和书中的一致。 Matlab代码如下。 运行示例的线性方程组是《数值计算方法》—丁丽娟 P-66 例一 运行结果如下: 若输入N=9,运行结果如下: 迭代的中间过程其中一小部分见下图: 注: 判断时否到达精度上限用的是范数,此处选用2范数,实际上选用1范数,inf范数均可,若想选用其他范数,调用norm(A,p)即可。
代码

// 输入量: A: 线性方程组的系数矩阵(n*n,非奇异) b: 方程组右边的常数项列向量 n: 方程组维数 x0: 初始值 tol: 精度上限值 N: 最大迭代次数 //迭代终止标准 已达精度上限值或者到达最大迭代次数 //输出量: x:线性方程组的解 // An highlighted block function x=jacobi_fun(A,b,n,x0,tol,N) x=zeros(n,1); % 给x赋值 k=0; while k<N for i=1:n x(i)=(b(i)-A(i,[1:i-1,i+1:n])*x0([1:i-1,i+1:n]))/A(i,i); end if norm(x-x0)<tol break; end x0=x; k=k+1; disp(['when k=',num2str(k)]) disp('x='); disp(x); %输出计算的中间结果 end if k==N disp('迭代次数已到达上限!'); end disp(['迭代次数 k=',num2str(k)]) end 运行
// Command Window 中输入 >> A=[10 -1 -2;-1 10 -2;-1 -1 5]; >> b=[72;83;42]; >> n=3; >> x0=[0;0;0]; >> tol=1e-6; >> N=500; // 输入后,调用函数 >> x=jacobi_fun(A,b,n,x0,tol,N)

可看出迭代16次之后得到精确值。

本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)