LeetCode 第 186 场周赛（1060/3107，前34.1%）数据结构与算法Michael是个半路程序员-

1. 比赛结果

做出来了 1、2 题，第3题模拟法，超时，第4题不会，继续加油！

全国排名：1060 / 3107，34.1%；全球排名：

2. 题目

1. LeetCode 5392. 分割字符串的最大得分 easy

题目链接

给你一个由若干 0 和 1 组成的字符串 s ，请你计算并返回将该字符串分割成两个 非空 子字符串（即 左 子字符串和 右 子字符串）所能获得的最大得分。

「分割字符串的得分」为 左 子字符串中 0 的数量加上 右 子字符串中 1 的数量。

示例 1： 输入：s = "011101" 输出：5  解释： 将字符串 s 划分为两个非空子字符串的可行方案有： 左子字符串 = "0" 且 右子字符串 = "11101"，得分 = 1 + 4 = 5  左子字符串 = "01" 且 右子字符串 = "1101"，得分 = 1 + 3 = 4  左子字符串 = "011" 且 右子字符串 = "101"，得分 = 1 + 2 = 3  左子字符串 = "0111" 且 右子字符串 = "01"，得分 = 1 + 1 = 2  左子字符串 = "01110" 且 右子字符串 = "1"，得分 = 2 + 1 = 3  示例 2： 输入：s = "00111" 输出：5 解释：当 左子字符串 = "00" 且 右子字符串 = "111" 时， 我们得到最大得分 = 2 + 3 = 5  示例 3： 输入：s = "1111" 输出：3   提示： 2 <= s.length <= 500 字符串 s 仅由字符 '0' 和 '1' 组成。 

解答：

• 左右两边，前缀0，后缀1，一次遍历即可
  
  比赛的时候写的有点繁琐

class Solution { public: int maxScore(string s) {         vector<int> left0(2*s.size()-1,0);         vector<int> right1(2*s.size()-1,0); int i, n = s.size();         left0[0] = s[0]=='0' ? 1 : 0; for(i = 1; i < n; ++i)             left0[2*i] = s[i]=='0'? left0[2*i-2]+1 : left0[2*i-2];                      right1[2*n-2] = s[n-1]=='1' ? 1 : 0; for(i = n-2; i >= 0; --i)             right1[2*i] = s[i]=='1'? right1[2*i+2]+1 : right1[2*i+2]; int maxsc = 0; for(i = 1; i < 2*n-2; i+=2)             maxsc = max(maxsc, left0[i-1]+right1[i+1]); return maxsc; } }; 

4 ms 6.9 MB

赛后解

class Solution { public: int maxScore(string s) { int i, one = 0, maxs = 0, zero = 0; for(i = 0; i < s.size(); ++i) { if(s[i]=='1')                 one++; } for(i = 0; i < s.size()-1; ++i) { if(s[i]=='0')                 zero++; else                 one--;             maxs = max(maxs,zero+one); } return maxs; } }; 

0 ms 6.4 MB

2. LeetCode 5393. 可获得的最大点数 medium

题目链接
几张卡牌 排成一行，每张卡牌都有一个对应的点数。
点数由整数数组 cardPoints 给出。

每次行动，你可以从行的开头或者末尾拿一张卡牌，最终你必须正好拿 k 张卡牌。

你的点数就是你拿到手中的所有卡牌的点数之和。

给你一个整数数组 cardPoints 和整数 k，请你返回可以获得的最大点数。

示例 1： 输入：cardPoints = [1,2,3,4,5,6,1], k = 3 输出：12 解释：第一次行动，不管拿哪张牌，你的点数总是 1 。 但是，先拿最右边的卡牌将会最大化你的可获得点数。 最优策略是拿右边的三张牌，最终点数为 1 + 6 + 5 = 12 。  示例 2： 输入：cardPoints = [2,2,2], k = 2 输出：4 解释：无论你拿起哪两张卡牌，可获得的点数总是 4 。  示例 3： 输入：cardPoints = [9,7,7,9,7,7,9], k = 7 输出：55 解释：你必须拿起所有卡牌，可以获得的点数为所有卡牌的点数之和。  示例 4： 输入：cardPoints = [1,1000,1], k = 1 输出：1 解释：你无法拿到中间那张卡牌，所以可以获得的最大点数为 1 。   示例 5： 输入：cardPoints = [1,79,80,1,1,1,200,1], k = 3 输出：202   提示： 1 <= cardPoints.length <= 10^5 1 <= cardPoints[i] <= 10^4 1 <= k <= cardPoints.length 

解答：

比赛的时候差点被坑，以为是DP，一想左右各取a，b个，a+b = k 不就完了吗
（也可以反过来想，求中间子序和最小，滑动窗口）

class Solution { public: int maxScore(vector<int>& cardPoints, int k) {         vector<int> l(k+2,0);         vector<int> r(k+2,0); int len = 1, i; for(i = 0; i < k; ++i,++len)             l[len] = cardPoints[i]+l[len-1];         len = 1; for(i = cardPoints.size()-1; len <= k; --i,++len)             r[len] = cardPoints[i]+r[len-1]; int maxScore = 0; for(len = 0; len <= k; ++len)             maxScore = max(maxScore, l[len]+r[k-len]); return maxScore; } }; 

148 ms 44.2 MB

3. LeetCode 5394. 对角线遍历 II medium

题目链接
给你一个列表 nums ，里面每一个元素都是一个整数列表。
请你依照下面各图的规则，按顺序返回 nums 中对角线上的整数。

示例 1：

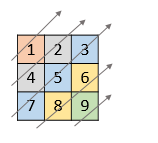
输入：nums = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,4,2,7,5,3,8,6,9] 

示例 2：

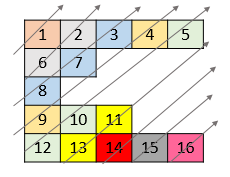
输入：nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]] 输出：[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]  示例 3： 输入：nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]] 输出：[1,4,2,5,3,8,6,9,7,10,11]  示例 4： 输入：nums = [[1,2,3,4,5,6]] 输出：[1,2,3,4,5,6]   提示： 1 <= nums.length <= 10^5 1 <= nums[i].length <= 10^5 1 <= nums[i][j] <= 10^9 nums 中最多有 10^5 个数字。 

比赛模拟写法超时：

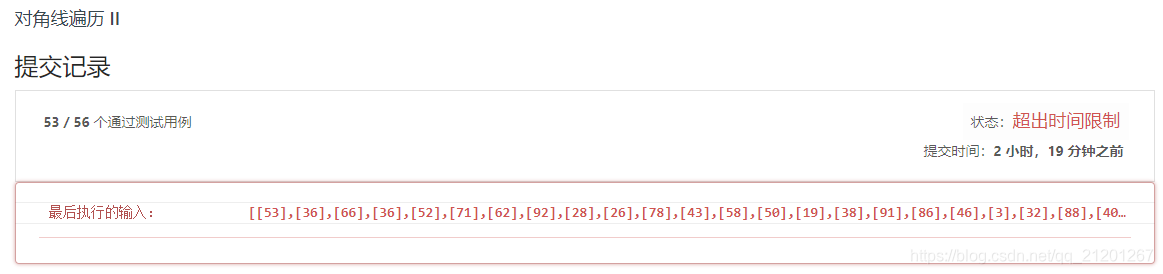
class Solution { public:     vector<int> findDiagonalOrder(vector<vector<int>>& nums) {         vector<int> ans; int i = 0, j = 0, count = 0, c = 0, x, y, m = nums.size(),n=0, finishi = -1;         vector<int> precount(nums.size(),0); for(i = 0; i < m; ++i) {             count += nums[i].size();//总个数             n = max(n, int(nums[i].size()));//列最大个数 }         x = y = i = j = 0; while(c < count) {             i = x, j = y;//x,y起始位置 while(i>=0 && j<n && c<count) { if(j < nums[i].size())//在范围内 {                     ans.push_back(nums[i][j]);                     c++;//计数+1                     precount[i]++;//该行写入答案数量+1 if(precount[i]==nums[i].size())//这行写完了 { if(precount[finishi+1] == nums[finishi+1].size())                             finishi++;//检查已完成的行，能不能往下挪 } }                 i--;                 j++; if(i <= finishi) break; }             x++; if(x >= m) {                 x = m-1;                 y++; } } return ans; } }; 

赛后解1：（依然超时）

实际上是按点的位置（r,c）排序：总的是r+c小的靠前，一样的话，r 大的靠前。

class Solution { public:     vector<int> findDiagonalOrder(vector<vector<int>>& nums) { int i, j;         vector<vector<int>> v; //posx+posy, posx, val for(i = 0; i < nums.size(); ++i) { for(j = 0; j < nums[i].size(); ++j) {                 v.push_back({i+j, i, nums[i][j]}); } } sort(v.begin(), v.end(),[&](auto a, auto b){ if(a[0]==b[0]) return a[1] > b[1]; return a[0] < b[0]; });         vector<int> ans(v.size());         i = 0; for(auto& vi : v)             ans[i++] = vi[2]; return ans; } }; 

估计是排序时间复杂度还是太高。

赛后解2：

• 按照两个坐标值的和分组，存入map，内层再嵌套map（x，val）
• 外层顺序遍历（坐标和小的先），内层逆序遍历（x大的先）

class Solution { public:     vector<int> findDiagonalOrder(vector<vector<int>>& nums) { int i, j, size = 0;         map<int,map<int,int>> m;//posx+posy, posx, val for(i = 0; i < nums.size(); ++i) { for(j = 0; j < nums[i].size(); ++j) {                 m[i+j][i] = nums[i][j];                 size++; } }                  vector<int> ans(size);         i = 0; for(auto it = m.begin(); it != m.end(); ++it) { for(auto it1 = it->second.rbegin(); it1 != it->second.rend(); ++it1)                 ans[i++] = it1->second; } return ans; } }; 

或者用数组做，参考lc题解，也是按坐标和分组，每组里面逆序写入答案。

4. LeetCode 5180. 带限制的子序列和 hard

题目链接

给你一个整数数组 nums 和一个整数 k ，请你返回 非空 子序列元素和的最大值，
子序列需要满足：子序列中每两个 相邻 的整数 nums[i] 和 nums[j] ，它们在原数组中的下标 i 和 j 满足 i < j 且 j - i <= k 。

数组的子序列定义为：将数组中的若干个数字删除（可以删除 0 个数字），剩下的数字按照原本的顺序排布。

示例 1： 输入：nums = [10,2,-10,5,20], k = 2 输出：37 解释：子序列为 [10, 2, 5, 20] 。  示例 2： 输入：nums = [-1,-2,-3], k = 1 输出：-1 解释：子序列必须是非空的，所以我们选择最大的数字。  示例 3： 输入：nums = [10,-2,-10,-5,20], k = 2 输出：23 解释：子序列为 [10, -2, -5, 20] 。   提示： 1 <= k <= nums.length <= 10^5 -10^4 <= nums[i] <= 10^4 

解答：

• 此题跟 LeetCode 239. 滑动窗口最大值（双端队列+单调栈） 非常类似，可以先看这题

• dp[i] 表示包含 i 位置的 最大子序和

• deque 里面保持递减状态（dp值递减，实际存储下标），距离超过 k 的，从队头出去

• 队头（最大的）>0，则 dp[i] = dp[q.front()]+nums[i]，否则，dp[i] = nums[i]

• 然后检查 dp[i] 要入队，队内是否单调递减，不满足，要pop_back()

class Solution { public: int constrainedSubsetSum(vector<int>& nums, int k) { int i, n = nums.size(), maxsum = INT_MIN;         vector<int> dp(n, 0);         dp[0] = nums[0];         maxsum = nums[0];         deque<int> q;         q.push_back(0); for(i = 1; i < n; i++) { if(i-q.front() > k)//距离超过k了           q.pop_front(); if(dp[q.front()] > 0)//最大的大于0，可以变大           dp[i] = dp[q.front()]+nums[i]; else//不能变大，自己就是自己                 dp[i] = nums[i];             maxsum = max(maxsum,dp[i]);//更新最大值 while(!q.empty() && dp[i] >= dp[q.back()])           q.pop_back();//不满足单点递减，pop_back          q.push_back(i); } return maxsum; } }; 

112 ms 14.7 MB