记一次自己动手实现一个简单神经网络

之前一直调包，最近刷算法题，就突发奇想，想自己试一试实现一个简单的神经网络模型。
从简单的开始，先实现一个二分类模型，使用印第安人糖料病数据集，数据集合源码可直接在github获取：github

参数初始化

首先，初始化参数，这里直接使用用numpy的初始化数组，代码如下：

 # 参数初始化 def inital_parameters(self, m, n):   res = [] for i in range(m):       res.append(np.random.randn(n)) return np.array(res) 

定义激活函数

神经网络中，每个神经元都有激活前和激活后的值，也可以认为是神经元的输入和输出，所以我们首先定义激活函数。本模型中，在第一层全连接层中使用sigmoid激活函数，第二层使用softmax激活函数输出结果，这里都是用numpy的内置方法计算，实现矩阵的并行化计算，具体公式可百度，代码如下：

 # sigmoid def sigmoid(self, x): return 1 / (1 + np.exp(-x)) # softmax def softmax(self, x):   x_exp = np.exp(x)   x_sum = np.sum(x_exp, axis=1, keepdims=True)   s = x_exp / x_sum   return s 

前向传播

全连接层的前向传播，简单来说就是参数与输入数据线性组合和输入神经元，经过激活函数后输出，要注意矩阵运算时的维度，代码如下：

 # 全连接层前向传播 def fully_connected_layer(self, x, layer):         x, w, b = np.array(x), np.array(self.ws[layer]), np.array(self.bs[layer]) assert len(x[0]) == len(w[0]) assert len(w) == len(b[0])         self.input.append(x)         pre_activation = np.sum([np.matmul(x, w.T), b], axis=0)         post_activation = self.activate[layer](pre_activation) return post_activation 

损失函数

由于是二分类与问题，这里使用交叉熵来计算损失函数，并记录初始梯度，代码如下：

 # 交叉熵损失函数 def cross_entropy(self, y_, Y):         loss = 0 # 记录初始梯度         w_gradients = [[0, 0]] for i in range(len(y_)):             predict = y_[i] for j in range(len(predict)): # +0.001，避免除0                 w_gradients[0][j] -= 1 / (predict[j] + 0.0001) if j == Y[i]:                     loss -= np.log(predict[j]) break         loss /= len(y_)         w_gradients[0][0] /= len(y_)         w_gradients[0][1] /= len(y_)         self.w_gradient.append(np.array(w_gradients))         self.b_gradient.append(np.array(w_gradients)) return loss 

实现BP(Backward Propagation)算法

BP(Backward Propagation)算法，也是整个神经网络中的最复杂的部分，其核心在于计算梯度时求导的链式法则，从神经网络最顶层开始，逐步向下层计算梯度，从而得到loss对于每一层参数的梯度。这里使用mini_batch梯度下降法，加快计算，其中将mini_batch置为1时就是SGD了，代码如下：

# BP算法 def backward_propagation(self, learning_rate, Y, mini_batch_size): # mini_batch gradient_descent for i in range(len(self.ws) - 1, -1, -1):             wi = self.ws[i]             bi = self.bs[i] # 初始化当前层w的梯度             w_gradients = [[0 for _ in range(len(wi[0]))] for _ in range(len(wi))] # 初始化当前层b的梯度             b_gradients = [[0 for _ in range(len(bi[0]))]] # 上一层的w梯度             w_last_gradient = self.w_gradient[len(self.ws) - i - 1] # 上一层b梯度             b_last_gradient = self.b_gradient[len(self.bs) - i - 1]              a_f_gra = self.activate_gradient[i] # mini_batch sample             sample = np.random.randint(len(Y), size=mini_batch_size) # 计算当前层w的梯度 for l in range(len(wi)):                 w = wi[l] for j in range(len(w)): for k in sample: input = self.input[i][k] for m in range(len(w_last_gradient)):                             w_gradients[l][j] += learning_rate * w_last_gradient[m][l] * a_f_gra(input, j) * input[j] # 计算当前层b的梯度 for l in range(len(bi)):                 b = bi[l] for j in range(len(b)): for k in sample: input = self.input[i][k] for m in range(len(b_last_gradient)):                             b_gradients[l][j] += learning_rate * b_last_gradient[m][l] * a_f_gra(input, j)              self.w_gradient.append(np.array(w_gradients))             self.b_gradient.append(np.array(b_gradients)) # 把初始梯度删去，然后因为是倒着添加梯度的，所以要倒过来         self.w_gradient.pop(0)         self.w_gradient = self.w_gradient[::-1]          self.b_gradient.pop(0)         self.b_gradient = self.b_gradient[::-1] # w梯度下降 for i in range(len(self.ws)):             wi = self.ws[i] for j in range(len(wi)):                 w = wi[j] for k in range(len(w)):                     self.ws[i][j][k] -= self.w_gradient[i][j][k] # b梯度下降 for i in range(len(self.bs)):             bi = self.bs[i] for j in range(len(bi)):                 b = bi[j] for k in range(len(b)):                     self.bs[i][j][k] -= self.b_gradient[i][j][k] # 一轮梯度下降后清空         self.w_gradient = []         self.b_gradient = []         self.input = [] 

训练和测试

首先读取数据，这里读取印第安人糖尿病数据集，总共768条数据，取前700条作为训练数据，后68条作为测试数据，代码如下：

 # 读取数据     filename = 'data/pima_data.csv'     names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']     data = read_csv(filename, names=names)     array = data.values     X = np.array(array[:, 0:8])     Y = array[:, 8]     X_normed = X / X.max(axis=0)      X_train = X_normed[:700]     X_test = X_normed[701:]      Y_train = Y[:700]     Y_test = Y[701:] 

接下来就是模型搭建和训练了，这里搭建两个全连接层，进行训练，代码如下：

 # 模型参数初始化     nn = NerualNetwork()     sigmoid = ActivationFunction().sigmoid     softmax = ActivationFunction().softmax      sigmoid_gradient = ActivationFunction().sigmoid_gradient     softmax_gradient = ActivationFunction().softmax_gradient      w1, b1 = nn.inital_parameters(5, 8), nn.inital_parameters(1, 5)     w2, b2 = nn.inital_parameters(2, 5), nn.inital_parameters(1, 2) # 导入初始化参数     nn.ws = [w1, w2]     nn.bs = [b1, b2] # 导入激活函数及其导数     nn.activate = [sigmoid, softmax]     nn.activate_gradient = [sigmoid_gradient, softmax_gradient] # 训练     epoch = 500     learning_rate = 0.005     mini_batch_size = 1     plot_x = []     plot_y = [] for i in range(epoch):         f_c1 = nn.fully_connected_layer(X_train, 0)         y_ = nn.fully_connected_layer(f_c1, 1)         train_loss = nn.cross_entropy(y_, Y_train) print('Epoch:', i + 1, ', train_loss=', train_loss)         plot_x.append(i + 1)         plot_y.append(train_loss)         nn.backward_propagation(learning_rate, Y_train, mini_batch_size)      plt.xlabel('Epoch')     plt.ylabel('loss')     plt.plot(plot_x, plot_y)     plt.show() 

训练结果为：
Epoch: 500 , train_loss= 0.6623333458935591

loss趋势图为：

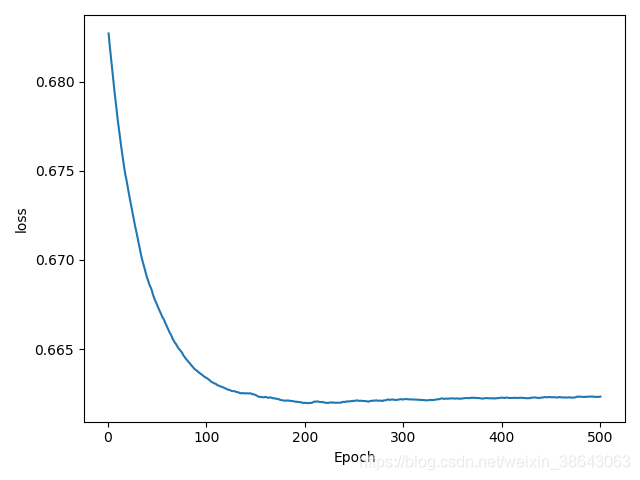
训练完成之后，将训练后的参数用于测试数据中进行测试，并计算准确率，代码如下：

 # 测试     f_c1 = nn.fully_connected_layer(X_test, 0)     y_ = nn.fully_connected_layer(f_c1, 1)     hit = 0 for i in range(len(y_)):         predict = list(y_[i])         pr = predict.index(max(predict)) if pr == Y_test[i]:             hit += 1     accuracy = hit / len(Y_test) print('accuracy=', accuracy) 

测试结果为：
accuracy= 0.5970149253731343

pytorch对比

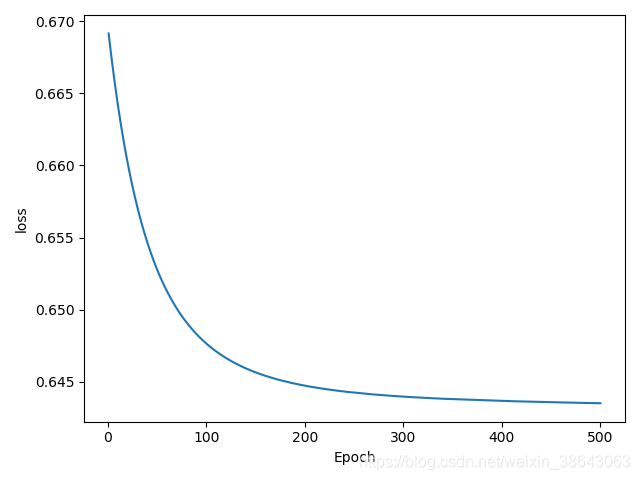
自己写的也不确定准不准确，所以就用pytorch来对比一下吧，当然要使用同样的超参数，然后这里就不阐述了，直接上代码：

 # 读取数据     filename = 'data/pima_data.csv'     names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']     data = read_csv(filename, names=names)     array = data.values     X = np.array(array[:, 0:8])     Y = np.array(array[:, 8])     X_normed = X / X.max(axis=0)      X_train = X_normed[:700]     X_test = X_normed[701:]      Y_train = Y[:700]     Y_test = Y[701:]      X_train = torch.tensor(X_train).float()     Y_train = torch.tensor(Y_train).long()      X_test = torch.tensor(X_test).float()     Y_test = torch.tensor(Y_test).long() # 搭建网络     myNet = nn.Sequential(         nn.Linear(8, 5, bias=True),         nn.Sigmoid(),         nn.Linear(5, 2, bias=True),         nn.Softmax() ) # 设置优化器     optimzer = torch.optim.SGD(myNet.parameters(), lr=0.005)     loss_func = nn.CrossEntropyLoss()     plot_x = []     plot_y = [] for epoch in range(500):         out = myNet(X_train)         loss = loss_func(out, Y_train) print('Epoch=', epoch+1, ' train_loss=', loss)         plot_x.append(epoch + 1)         plot_y.append(loss)          optimzer.zero_grad()         loss.backward()         optimzer.step()      plt.xlabel('Epoch')     plt.ylabel('loss')     plt.plot(plot_x, plot_y)     plt.show()      y_ = np.array(myNet(X_test).data)      hit = 0 for i in range(len(y_)):         predict = list(y_[i])         pr = predict.index(max(predict)) if pr == Y_test[i]:             hit += 1     accuracy = hit / len(Y_test) print('accuracy=', accuracy) 

pytorch的训练结果：
Epoch= 500 train_loss= tensor(0.6753)

pytorch的loss趋势图为：

测试结果为：
accuracy= 0.5970149253731343

惊了，这里准确率的结果居然和我自己写的一模一样，绝对没有造假，不过应该是测试数据不够多的原因。

缺陷与不足

这里算是完整的自己手动实现了一个简单的神经网络，当然还存在很多缺陷与不足：
（1）参数的初始化不够好
（2）梯度下降时没有使用矩阵并行计算，这里怕写错，所以暂时直接用的for循环，之后再看看修改
（3）训练未设置收敛条件
（4）BP实现的比较仓促，肯定还有很多细节问题，导致我的loss比较陡峭
（5）肯定还有很多很多很多很多问题，请批评指正
（6）肯定还有很多很多很多很多问题，请批评指正
（7）肯定还有很多很多很多很多问题，请批评指正
。。。。。。

另外也是第一次写博客，写的不好请见谅，也请批评指正