参考:https://www.zhihu.com/question/367466399?from=groupmessage 假设在某时刻t上,易感者为S(t),感染者为:I(t),康复者(有抗体)为R(t)。 预备知识: 在 SI 模型里面,只考虑了易感者和感染者,并且感染者不能够恢复,此类病症有 HIV 等; 假定:总人口数为N(t)=S(t)+I(t),疾病流行期间,人口的出生率和自然死亡率分别为 用微分方程的式子表达 除了 HIV 这种比较严重的病之外,还有很多小病是可以恢复并且反复感染的,例如日常的感冒,发烧等。在这种情况下,感染者就有一定的几率重新转化成易感者。如下图所示: 有的时候,感染者在康复之后,就有了抗体,于是后续就不会再获得此类病症,这种时候,考虑SIS模型就不再合适了,需要考虑SIR模型。此类病症有麻疹,腮腺炎,风疹等。 对于这类方程,就不能够得到其解析解了,只能够从它的动力系统开始进行分析,得到解的信息。根据第一个微分方程可以得到 通过对 SEIR 模型的研究, 可以预测一个封闭地区疫情的爆发情况, 最大峰值, 感染人数等等 但是显然没有任何地区是封闭的, 所以就要把各个地区看成图的节点, 地区之间的流动可以由马尔可夫转移所刻画, 对每个结点单独跑 SEIR 模型. 最后整个仿真模型就可以比较准确的反应疫情的散播和爆发情况 当然可以再加入更多的决策因素。
假定人群分为4种,分别是:
那麽在时刻t,总人口数为N(t)=S(t)+I(t)+R(t)。如果暂时不考虑人口的增加和死亡的情况,那么N(t)=N是一个恒定的值。
除此之外:
r表示在单位时间内感染者接触到的易感者人数;
β表示感染者接触到易感者之后,易感者得病的概率;
γ表示感染者康复的概率,有可能变成易感者S(可再感染),也有可能变成康复者R(不再感染)。
假设
x=x(t)是关于
t的一个方程,且满足
dtdx+a1x+a2x2=0和
x(0)=x0,那么它的解为:
x(t)=x01−a1a2(e−a1t−1)e−a1t。

四类传染病模型:
SI模型
由于艾滋传染之后不可治愈,所以该模型为:易感染者被感染。
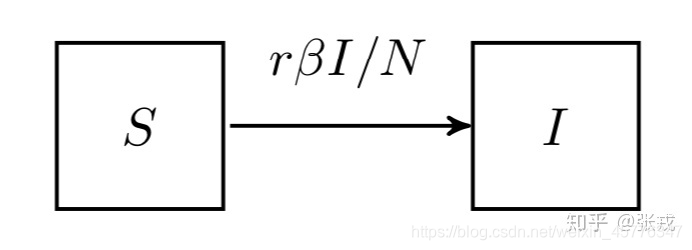
μ 和
ν,不考虑因病死亡,新增人都是易感染者,感染人数为
NβSI
{dtdS=−NrβISdtdI=NrβIS
初始条件是
S(t)=S0,I(0)=I0,并且
N(t)=S(t)+I(t)对于所有的
t≥0都成立。
于是,把
S=N−I代入第二个微分方程中,最后常微分方程的解为:
I(t)=I0+(N−I0)e−rβtNI0
这就是所谓的逻辑回归函数,而在机器学习领域,最简单的逻辑回归函数为
σ(x)=1+e−x1,而
I(t)只是做了一些坐标轴的平移和压缩而已。由于
limt→+∞e−t=0,所以
limt→+∞I(t)=N,从而
limt→+∞S(t)=0
通过数值模拟可以进一步知道:
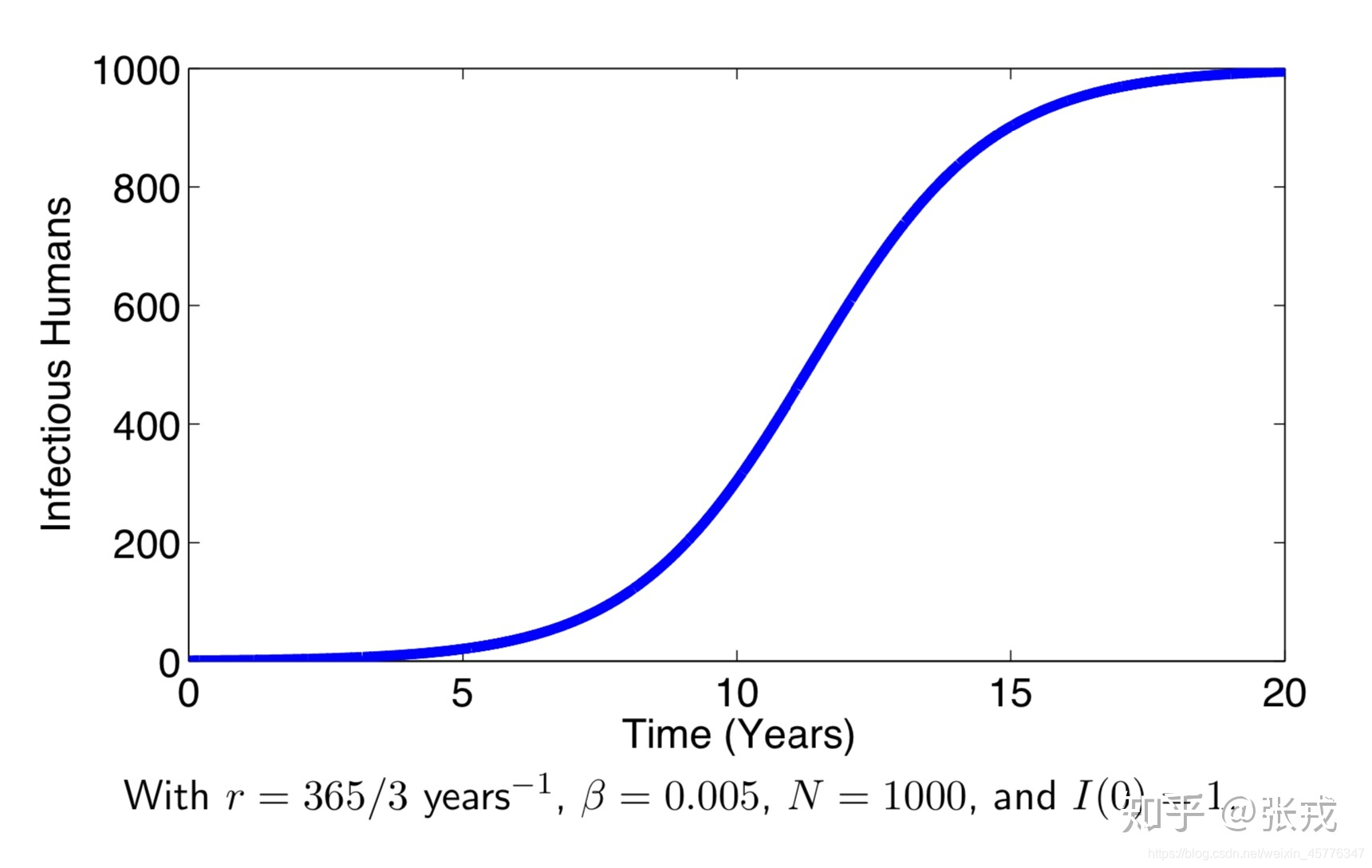
此处最好的办法应该是用拟和优化。
简单来看,再SI模型下,最后全部的人群都会被感染。SIS模型
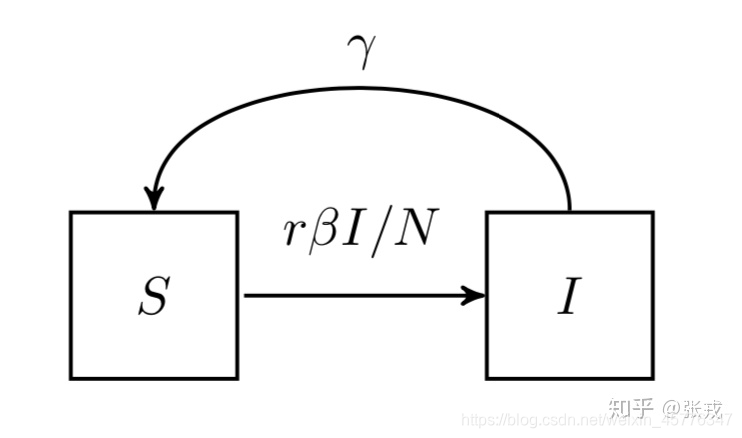 其微分方程就是:
其微分方程就是:
{dtdS=−NrβSI+γIdtdI=NrβSI−γI其初始条件为
S(0)=S0,I(0)=I0。
是用同样的办法,把
S=N−I导入第二个微分方程。最后得到的最终解为
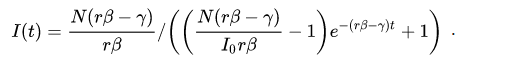
从而也得到
limt→+∞I(t)=rβN(rβ−γ),且
limt→+∞S(t)=rβNγ,这个方程同样也是逻辑回归方程,只是它的渐近线与之前的SI模型有所不同。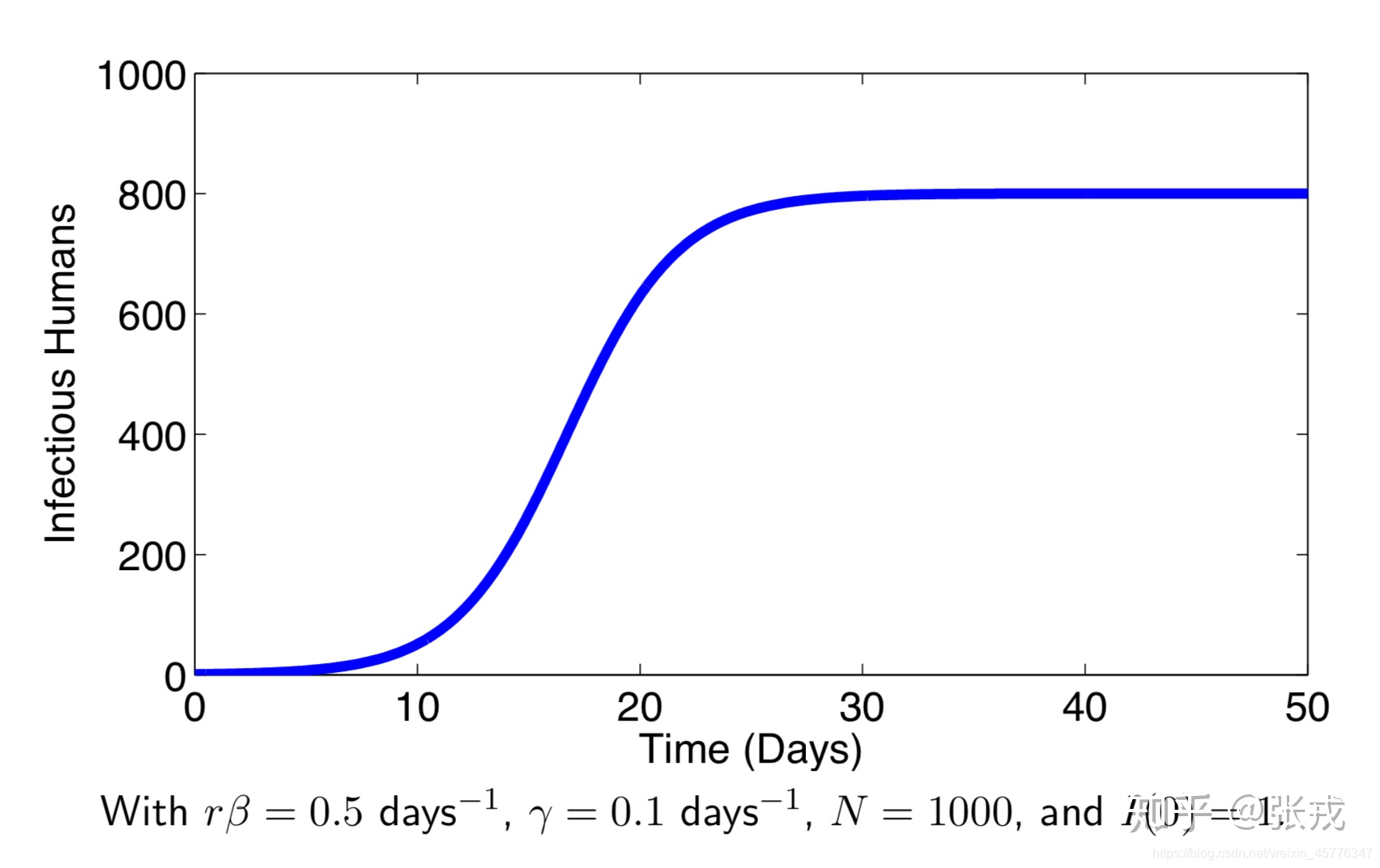
SIR模型
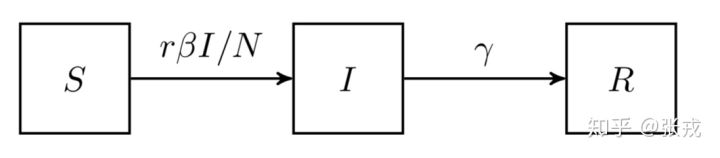 其微分方程是:
其微分方程是:
⎩⎨⎧dtdS=−NrβSIdtdI=NrβSI−γIdtdR=γI
其初始条件是
S(0)=S0,I(0)=I0,R(0)=R0,并且
S(t),I(t),R(t)≥0和
S(t)+I(t)+R(t)=N对于所有的
t≥0都成立。
dtdS=−NrβSI<0 ,于是
S(t) 是一个严格递减函数,同时,
0≤S(t)≤N 对于所有的
t≥0 都成立,于是存在
S∞∈[0,+∞],使得
limt→+∞S(t)=S∞
通过第一个微分方程和第二个微分方程可以得到:
dtd(S+I)=−γI,因此对它两边积分得到
 由于
由于
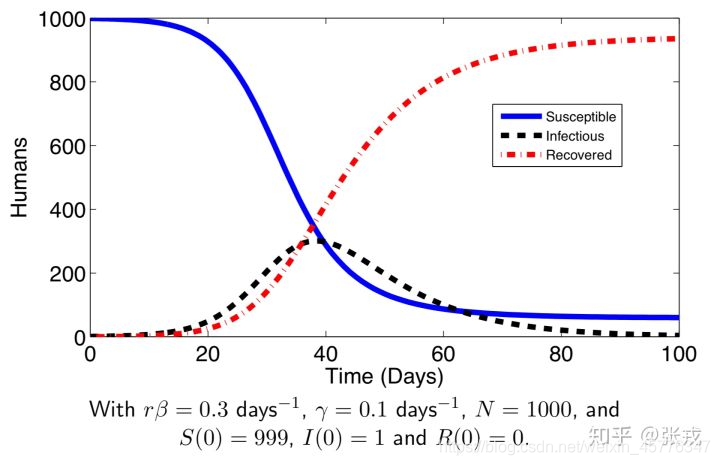
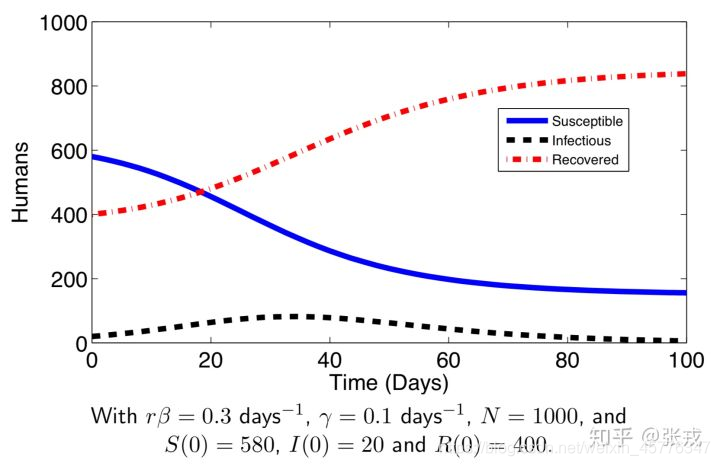
S(t)是严格单调递减函数,因此从第二个微分方程可以得到:当
S(t)=rβNγ时,感染人数
I(t)达到最大值。
SEIR模型
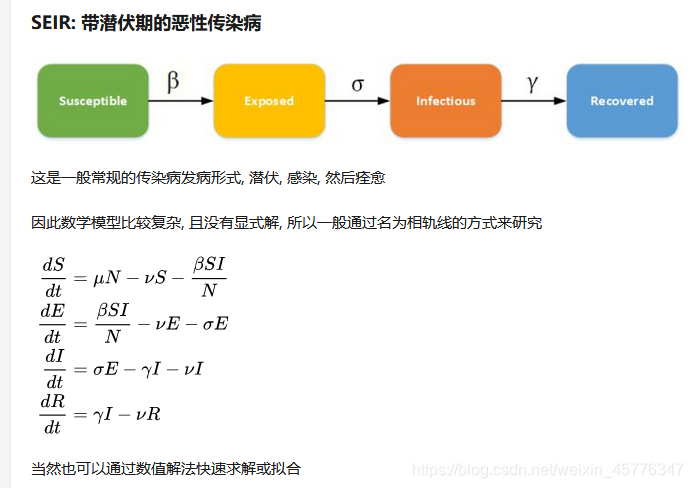 注意此处的SEIR模型加入了扰动因子v,前面三种模型也可以加入扰动因子,加入扰动因子的模型往往更合理。
注意此处的SEIR模型加入了扰动因子v,前面三种模型也可以加入扰动因子,加入扰动因子的模型往往更合理。
原因:就拿SEIR模型来说,
它不是万能的,总有一些异常状况,如有的人潜伏期短,有的人潜伏期长,还可能有超级感染者,有的潜伏者可能就直接痊愈了,变成了抵抗者。方程并没有单独处理这些情况,因为一定程度内这些异类都可以被扰动因子所包含。研究一个固定的模型加扰动项,比不断地往模型里加扰动项好研究的多。