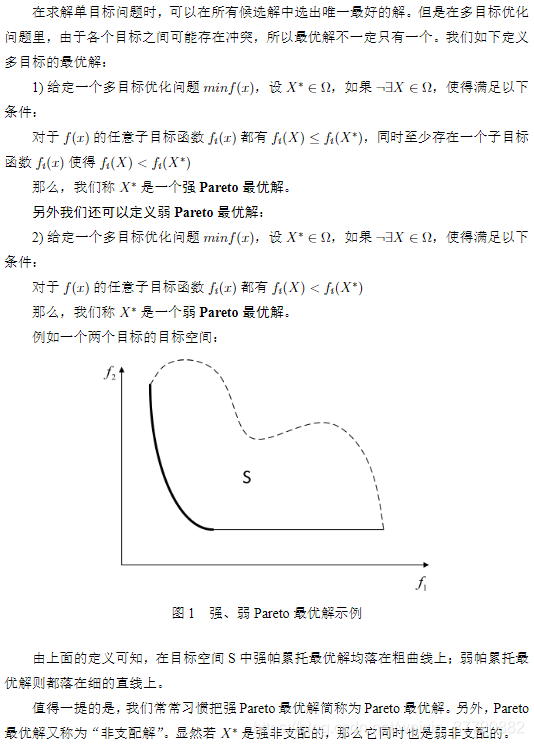
目录 自从上三篇博客详细讲解了Python遗传和进化算法工具箱及其在带约束的单目标函数值优化中的应用、利用遗传算法求解有向图的最短路径、利用进化算法优化SVM参数之后,这篇不再局限于单一的进化算法工具箱的讲解,相反,这次来个横向对比,比较目前最流行的几个python进化算法工具箱/框架在求解多目标问题上的表现。 首先大致讲一下多目标优化: 在生活中的优化问题,往往不只有一个优化目标,并且往往无法同时满足所有的目标都最优。例如工人的工资与企业的利润。那么多目标优化里面什么解才算是优秀的?我们一般采用“帕累托最优”来衡量解是否优秀,其定义我这里摘录百度百科的一段话: 帕累托最优(Pareto Optimality),是指资源分配的一种理想状态。假定固有的一群人和可分配的资源,从一种分配状态到另一种状态的变化中,在没有使任何人境况变坏的前提下,使得至少一个人变得更好。帕累托最优状态就是不可能再有更多的帕累托改进的余地;换句话说,帕累托改进是达到帕累托最优的路径和方法。 帕累托最优是公平与效率的“理想王国”。是由帕累托提出的。 这段话好像让人看着依旧有点懵逼,下面直接摘录一段学术性的定义: 因此,只要找到一组解,其对应的待优化目标函数值的点均落在上面的黑色加粗线上,那么就是我们想要的“帕累托最优解”了。此外,假如帕累托最优解个数不可数,那么我们只需找到上面黑色加粗线上的若干个点即可,并且这些点越分散、分布得越均匀,说明算法的效果越好。 多目标进化优化算法即利用进化算法结合多目标优化策略来求解多目标优化问题。经典而久经不衰的多目标优化算法有:NSGA2、NSGA3、MOEA/D等。其中NSGA2和NSGA3是基于支配的MOEA(Multi-objective evolutionary algorithm),而MOEA/D是基于分解的MOEA。 前两者(NSGA2、NSGA3)通过非支配排序(后面马上讲到)来筛选出一堆解中的“非支配解”,并且通过种群的不断进化,使得种群个体对应的解对应的目标函数值的点不断逼近上图的黑色加粗线。具体算法就不作详细阐述了,可详见以下参考文献,或看下方的代码实战部分: Deb K , Pratap A , Agarwal S , et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2):0-197. Deb K , Jain H . An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601. 后者(MOEA/D)通过线性或非线性的方式将原多目标问题中各个目标进行聚合,即将多个目标聚合成一个目标,然后利用种群进化不断逼近全局帕累托最优解。这里可能有人会有疑问:“为什么MOEA/D是基于分解的MOEA,但过程中需要对各个目标进行聚合?那不就不叫分解了吗?”答案很简单:分解是指将多目标优化问题分解为一组单目标子问题或多个多目标子问题,利用子问题之间的邻域关系,通过协作来同时优化所有的子问题,从而不断逼近全局帕累托最优解;而聚合是指将多个目标聚合成一个目标,因此MOEA/D里面有“分解”和“聚合”两个步骤,分解是确定邻域关系,聚合是用来方便比较解的优劣,两者并不是矛盾的。具体算法就不作详细阐述了,可详见以下参考文献,或看下方的代码实战部分: Qingfu Zhang, Hui Li. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition[M]. IEEE Press, 2007. 那么存在只利用聚合而没有分解这一步来进化优化的算法吗?答案是存在的,比如多目标优化自适应权重法(awGA),代码详见链接: https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/awGA/moea_awGA_templet.py 这个算法就是通过自适应地生成一个权重向量,来将所有的优化目标聚合成单一的优化目标,然后进行进化优化,当然这样效果自然比不上MOEA/D。 有些单目标优化学得比较溜的读者可能会疑问:”我找一组固定的权重,把各个优化目标加权聚合成一个目标,再用单目标优化的方法进行优化不就完事了吗?“答案非常简单:如果有理论能证明所找的这组权重是最合理、最适合当前的优化模型的,那么用单目标优化的方法来解决多目标优化问题当然是好事;相反,假如没有依据地随便设置一组权重,那么肯定不能用这种方法。 下面以一个双目标优化测试函数ZDT1和一个三目标优化测试函数DTLZ1为例,横向对比deap、pymoo和geatpy三款进化算法代码包的NSGA2、NSGA3和MOEA/D算法的表现,版本分别为1.3、0.4.0、2.5.0,测试代码均为三款代码包官网给出的案例(在代码组织结构上稍作修改以方便本文显示)。 【注】:由于在计算ZDT1和DTLZ1时deap默认采用的是循环来计算种群中每个个体的目标函数值,而pymoo和geatpy均为利用numpy来矩阵化计算的,为了统一个体评价时间,避免前者带来的性能下降,这里将deap也改用与后两者相同的方法。 实验设备:cpu i5 9600k,16g ddr4内存,windows10,Python 3.7 x64。 相关库的安装: ZDT1的模型为: DTLZ1的模型为: 其中M为待优化的目标个数,y为决策变量。 下面用NSGA2算法来优化上面的ZDT1,实验参数为:【种群个体数40,进化代数200,其他相关参数均设为一样】,代码1、代码2、代码3分别为用deap、pymoo和geatpy的nsga2来优化ZDT1: 代码 1. deap_nsga2.py 上述代码1利用deap提供的进化算法框架来实现NSGA2算法。deap的主要特点是轻量化和支持扩展。整个deap内部的代码量很少,可以通过”函数注册“来扩展模块,但由此带来的结果便是需要自己写大量的代码。比如要在deap上写一个基因表达式编程(GEP),以geppy这个GEP框架为例,它除了使用到了deap中的”函数注册“功能(方便模块调用)外,几乎等于重写了一遍deap。 代码2:pymoo_nsga2.py 上述代码2调用了pymoo内置的NSGA2算法模块,不过该模块与pymoo框架深度耦合,无法直观地看到NSGA2的执行过程,非pymoo开发者想要在上面扩展自己设计的算法会遇到较大的困难。 代码3:geatpy_nsga2.py 上面代码3调用了Geatpy内置的NSGA2算法模板,见链接: https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/nsga2/moea_NSGA2_templet.py 该算法模板代码与Geatpy提供的进化算法框架的耦合度很小,可以清晰地看到NSGA2算法的执行过程。只需遵循Geatpy中设计的种群数据结构(如染色体用什么表示、目标函数值用什么表示、约束用什么表示),就能很容易在上面扩展自己设计的新进化算法。 此外由代码3可以看到使用Geatpy时可以更加专注于待优化模型的建立,即在做进化算法的应用时,不用管进化算法的细节,而专注于把待优化模型写成一个自定义问题类。 代码1、2、3的运行结果如下图: 下面用NSGA3算法来优化上面的DTLZ1,【种群个体数91,进化代数500,其他相关参数均设为一样】,代码4、代码5、代码6分别为用deap、pymoo和geatpy的nsga3来优化DTLZ1: 代码4:deap_nsga3.py 代码5:pymoo_nsga3.py 代码6:geatpy_nsga3.py 上面代码6调用了Geatpy内置的NSGA3算法模板,见链接: https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/nsga3/moea_NSGA3_templet.py 代码4、5、6的运行结果如下图: 下面用MOEA/D算法来优化上面的ZDT1,【种群个体数40,进化代数300,其他相关参数均设为一样】,由于deap并无提供MOEA/D的代码,因此这里只比较pymoo和geatpy。 值得注意的是:理论上MOEA/D会比NSGA2快,但由于python语言的限制,MOEA/D的算法设计在python上的执行效率会大打折扣。这种情况同样存在于Matlab中。如果是纯C/C++或者Java等,MOEA/D的高效率才能够真正展现出来。当然,假如在C/C++或Java中采用细粒度的并行来执行进化,那么MOEA/D的执行效率是远远比不上NSGA2的,这是因为MOEA/D的算法设计天然地不支持细粒度的并行。 下面的代码7、代码8分别为用pymoo和geatpy的MOEA/D来优化ZDT1的代码: 代码7:pymoo_moead.py 代码8:geatpy_moead.py 上面代码8调用了Geatpy内置的MOEA/D算法模板,见链接: https://github.com/geatpy-dev/geatpy/blob/master/geatpy/templates/moeas/moead/moea_MOEAD_templet.py 代码7、8的运行结果如下: 这里比较奇怪的是pymoo的基于切比雪夫法的MOEA/D经常会出现一个很差的解,如上面左图的最左边的点,应该是该版本(0.4.0)有BUG。 下面加大计算规模,比较deap、pymoo和geatpy在大规模种群下的表现。 先将代码1、2、3中种群规模调整为500,进化代数依旧是300,运行结果如下: 再将代码2、3、4中种群规模调整为496,进化代数依旧是500,运行结果如下: 更多比较结果见下表,这里增添4个经典的EA框架/平台:Pygmo、Pagmo、JMetal和Platemo来共同参与对比,各实验参数均保持一致。其中Pygmo的底层是Pagmo,顶层用Python代码驱动;Pagmo是纯C++的EA框架;JMetal是Java的EA框架;Platemo是Matlab的MOEA实验与测试平台。 此外需要注明的是本次实验中除了Pymoo和Platemo在大规模计算下会自动使用CPU并行计算外,其余框架的测试均不会自动使用CPU进行并行计算。其中Pagmo可以利用C++的Eigen矩阵库来加速进化计算,但众所周知Eigen速度不及Matlab的MKL矩阵库,且鉴于实验环境配置复杂,这里就没有使用Pagmo的矩阵计算了。 Deap Pymoo Geatpy Pygmo (C++) Pagmo(C++) JMetal (Java) Platemo (Matlab) ZDT1 NSGA2 1000个体300代 585.83秒 41.95秒 1.22秒 19.45秒 10.42秒 15.18秒 4.28秒 NSGA2 1万个体300代 >13小时 3587.65秒 20.70秒 2047.30秒 933.64秒 2738.85秒 86.16秒 3维DTLZ1 NSGA3 990个体500代 143.33秒 123.54秒 13.47秒 不支持 不支持 53.182秒 31.86秒 NSGA3 9870个体500代 15635.71秒 11542.05秒 1297.25秒 不支持 不支持 6316.710秒 2576.09秒 在上面的各个实验中没有计算多目标优化的各项评价指标,但从图便可大致推断效果的好坏。其中性能大幅领先于其他的是国产的Geatpy和Platemo,这是因为Geatpy的种群进化过程采用的是Geatpy团队自主研发的超高性能矩阵库进行计算(注:由于Geatpy尚未提供一个单一的标签来设置是否采用内核并行,上面的实验为了图方便均没使用Geatpy的内核并行);而Platemo利用Matlab自带的高性能矩阵库MKL进行计算(在大规模下会智能地采用CPU并行计算)。 本文比较了几种经典的进化算法框架/工具箱/平台在多目标优化上的表现。由于都具有权威性和各自的特色,这里我不作好坏对比,即不评价孰优孰劣,也不强行说推荐一定要用哪个,一切以自己习惯的编程语言为主。 不过如果读者有将进化计算与机器学习、神经网络、深度学习结合的需求,我在此建议使用Python的进化算法框架。用Python的话编程效率高,并且Python作为一种胶水语言,可以很容易嵌套进各种实际应用项目中,同时由上面的实验也可看出某些Python进化算法框架/工具箱也能达到乃至超越Java、C/C++的进化算法框架的执行速度(如Geatpy)。
前言
正文
1 多目标优化概念
2 多目标进化优化算法
3 代码实战
pip install deap pip install pymoo pip install geatpy
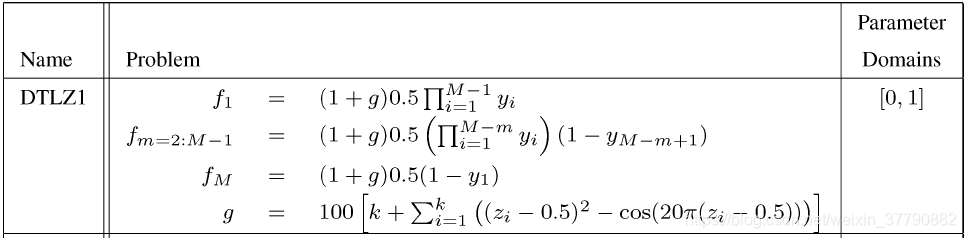
3.1 用NSGA2 优化 ZDT1
import array import random from deap import base from deap import creator from deap import tools import numpy as np import matplotlib.pyplot as plt import time def ZDT1(Vars, NDIM): # 目标函数 ObjV1 = Vars[:, 0] gx = 1 + 9 * np.sum(Vars[:, 1:], 1) / (NDIM - 1) hx = 1 - np.sqrt(np.abs(ObjV1) / gx) # 取绝对值是为了避免浮点数精度异常带来的影响 ObjV2 = gx * hx return np.array([ObjV1, ObjV2]).T creator.create("FitnessMin", base.Fitness, weights=(-1.0, -1.0)) creator.create("Individual", array.array, typecode='d', fitness=creator.FitnessMin) toolbox = base.Toolbox() # Problem definition BOUND_LOW, BOUND_UP = 0.0, 1.0 NDIM = 30 def uniform(low, up, size=None): try: return [random.uniform(a, b) for a, b in zip(low, up)] except TypeError: return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)] toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM) toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float) toolbox.register("population", tools.initRepeat, list, toolbox.individual) toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=20.0) toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=20.0, indpb=1.0/NDIM) toolbox.register("select", tools.selNSGA2) def main(seed=None): random.seed(seed) NGEN = 300 MU = 40 CXPB = 1.0 pop = toolbox.population(n=MU) # Evaluate the individuals with an invalid fitness invalid_ind = [ind for ind in pop if not ind.fitness.valid] ObjV = ZDT1(np.array(invalid_ind), NDIM) for ind, i in zip(invalid_ind, range(MU)): ind.fitness.values = ObjV[i, :] # This is just to assign the crowding distance to the individuals # no actual selection is done pop = toolbox.select(pop, len(pop)) # Begin the generational process for gen in range(1, NGEN): # Vary the population offspring = tools.selTournamentDCD(pop, len(pop)) offspring = [toolbox.clone(ind) for ind in offspring] for ind1, ind2 in zip(offspring[::2], offspring[1::2]): if random.random() <= CXPB: toolbox.mate(ind1, ind2) toolbox.mutate(ind1) toolbox.mutate(ind2) del ind1.fitness.values, ind2.fitness.values # Evaluate the individuals with an invalid fitness invalid_ind = [ind for ind in offspring if not ind.fitness.valid] ObjV = ZDT1(np.array([ind for ind in offspring if not ind.fitness.valid]), NDIM) for ind, i in zip(invalid_ind, range(MU)): ind.fitness.values = ObjV[i, :] # Select the next generation population pop = toolbox.select(pop + offspring, MU) return pop if __name__ == "__main__": start = time.time() pop = main() end = time.time() p = np.array([ind.fitness.values for ind in pop]) plt.scatter(p[:, 0], p[:, 1], marker="o", s=10) plt.grid(True) plt.show() print('耗时:', end - start, '秒')
from pymoo.algorithms.nsga2 import NSGA2 from pymoo.factory import get_problem from pymoo.optimize import minimize import matplotlib.pyplot as plt import time problem = get_problem("ZDT1") algorithm = NSGA2(pop_size=40, elimate_duplicates=False) start = time.time() res = minimize(problem, algorithm, ('n_gen', 300), verbose=False) end = time.time() plt.scatter(res.F[:, 0], res.F[:, 1], marker="o", s=10) plt.grid(True) plt.show() print('耗时:', end - start, '秒')
# -*- coding: utf-8 -*- import numpy as np import geatpy as ea class ZDT1(ea.Problem): # 继承Problem父类 def __init__(self): name = 'ZDT1' # 初始化name(函数名称,可以随意设置) M = 2 # 初始化M(目标维数) maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标) Dim = 30 # 初始化Dim(决策变量维数) varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数) lb = [0] * Dim # 决策变量下界 ub = [1] * Dim # 决策变量上界 lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含) ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含) # 调用父类构造方法完成实例化 ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin) def aimFunc(self, pop): # 目标函数 Vars = pop.Phen # 得到决策变量矩阵 ObjV1 = Vars[:, 0] gx = 1 + 9 * np.sum(Vars[:, 1:], 1) / (self.Dim - 1) hx = 1 - np.sqrt(np.abs(ObjV1) / gx) # 取绝对值是为了避免浮点数精度异常带来的影响 ObjV2 = gx * hx pop.ObjV = np.array([ObjV1, ObjV2]).T # 把结果赋值给ObjV if __name__ == "__main__": """================================实例化问题对象=============================""" problem = ZDT1() # 生成问题对象 """==================================种群设置================================""" Encoding = 'RI' # 编码方式 NIND = 40 # 种群规模 Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器 population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化) """================================算法参数设置===============================""" myAlgorithm = ea.moea_NSGA2_templet(problem, population) # 实例化一个算法模板对象 myAlgorithm.MAXGEN = 300 # 最大进化代数 myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制过程动画) """===========================调用算法模板进行种群进化=========================== 调用run执行算法模板,得到帕累托最优解集NDSet。NDSet是一个种群类Population的对象。 NDSet.ObjV为最优解个体的目标函数值;NDSet.Phen为对应的决策变量值。 详见Population.py中关于种群类的定义。 """ NDSet = myAlgorithm.run() # 执行算法模板,得到非支配种群 print('用时:%f 秒'%(myAlgorithm.passTime))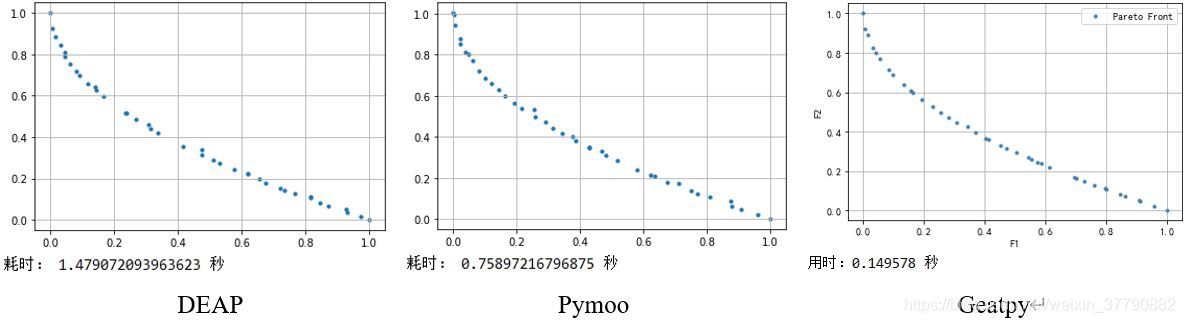
3.2 用NSGA3 优化 DTLZ1
from math import factorial import random import matplotlib.pyplot as plt import numpy as np from deap import algorithms from deap import base from deap import creator from deap import tools import matplotlib.pyplot as plt import mpl_toolkits.mplot3d as Axes3d import time # Problem definition NOBJ = 3 K = 5 NDIM = NOBJ + K - 1 P = 12 H = factorial(NOBJ + P - 1) / (factorial(P) * factorial(NOBJ - 1)) BOUND_LOW, BOUND_UP = 0.0, 1.0 def DTLZ1(Vars, NDIM): # 目标函数 XM = Vars[:,(NOBJ-1):] g = 100 * (NDIM - NOBJ + 1 + np.sum(((XM - 0.5)**2 - np.cos(20 * np.pi * (XM - 0.5))), 1, keepdims = True)) ones_metrix = np.ones((Vars.shape[0], 1)) f = 0.5 * np.hstack([np.fliplr(np.cumprod(Vars[:,:NOBJ-1], 1)), ones_metrix]) * np.hstack([ones_metrix, 1 - Vars[:, range(NOBJ - 2, -1, -1)]]) * (1 + g) return f ## # Algorithm parameters MU = int(H) NGEN = 500 CXPB = 1.0 MUTPB = 1.0/NDIM ## # Create uniform reference point ref_points = tools.uniform_reference_points(NOBJ, P) # Create classes creator.create("FitnessMin", base.Fitness, weights=(-1.0,) * NOBJ) creator.create("Individual", list, fitness=creator.FitnessMin) # Toolbox initialization def uniform(low, up, size=None): try: return [random.uniform(a, b) for a, b in zip(low, up)] except TypeError: return [random.uniform(a, b) for a, b in zip([low] * size, [up] * size)] toolbox = base.Toolbox() toolbox.register("attr_float", uniform, BOUND_LOW, BOUND_UP, NDIM) toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.attr_float) toolbox.register("population", tools.initRepeat, list, toolbox.individual) toolbox.register("mate", tools.cxSimulatedBinaryBounded, low=BOUND_LOW, up=BOUND_UP, eta=30.0) toolbox.register("mutate", tools.mutPolynomialBounded, low=BOUND_LOW, up=BOUND_UP, eta=20.0, indpb=1.0/NDIM) toolbox.register("select", tools.selNSGA3, ref_points=ref_points) ## def main(seed=None): random.seed(seed) # Initialize statistics object pop = toolbox.population(n=MU) # Evaluate the individuals with an invalid fitness invalid_ind = [ind for ind in pop if not ind.fitness.valid] ObjV = DTLZ1(np.array(invalid_ind), NDIM) for ind, i in zip(invalid_ind, range(MU)): ind.fitness.values = ObjV[i, :] # Begin the generational process for gen in range(1, NGEN): offspring = algorithms.varAnd(pop, toolbox, CXPB, MUTPB) # Evaluate the individuals with an invalid fitness invalid_ind = [ind for ind in offspring if not ind.fitness.valid] ObjV = DTLZ1(np.array([ind for ind in offspring if not ind.fitness.valid]), NDIM) for ind, i in zip(invalid_ind, range(MU)): ind.fitness.values = ObjV[i, :] # Select the next generation population from parents and offspring pop = toolbox.select(pop + offspring, MU) return pop if __name__ == "__main__": start = time.time() pop = main() end = time.time() fig = plt.figure() ax = fig.add_subplot(111, projection="3d") p = np.array([ind.fitness.values for ind in pop]) ax.scatter(p[:, 0], p[:, 1], p[:, 2], marker="o", s=10) ax.view_init(elev=30, azim=45) plt.grid(True) plt.show() print('耗时:', end - start, '秒')
from pymoo.algorithms.nsga3 import NSGA3 from pymoo.factory import get_problem, get_reference_directions from pymoo.optimize import minimize from pymoo.visualization.scatter import Scatter import time # create the reference directions to be used for the optimization M = 3 ref_dirs = get_reference_directions("das-dennis", M, n_partitions=12) N = ref_dirs.shape[0] # create the algorithm object algorithm = NSGA3(pop_size=N, ref_dirs=ref_dirs) start = time.time() # execute the optimization res = minimize(get_problem("dtlz1", n_obj = M), algorithm, termination=('n_gen', 500)) end = time.time() Scatter().add(res.F).show() print('耗时:', end - start, '秒')
# -*- coding: utf-8 -*- import numpy as np import geatpy as ea class DTLZ1(ea.Problem): # 继承Problem父类 def __init__(self, M): name = 'DTLZ1' # 初始化name(函数名称,可以随意设置) maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标) Dim = M + 4 # 初始化Dim(决策变量维数) varTypes = np.array([0] * Dim) # 初始化varTypes(决策变量的类型,0:实数;1:整数) lb = [0] * Dim # 决策变量下界 ub = [1] * Dim # 决策变量上界 lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含) ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含) # 调用父类构造方法完成实例化 ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin) def aimFunc(self, pop): # 目标函数 Vars = pop.Phen # 得到决策变量矩阵 XM = Vars[:,(self.M-1):] g = 100 * (self.Dim - self.M + 1 + np.sum(((XM - 0.5)**2 - np.cos(20 * np.pi * (XM - 0.5))), 1, keepdims = True)) ones_metrix = np.ones((Vars.shape[0], 1)) f = 0.5 * np.hstack([np.fliplr(np.cumprod(Vars[:,:self.M-1], 1)), ones_metrix]) * np.hstack([ones_metrix, 1 - Vars[:, range(self.M - 2, -1, -1)]]) * (1 + g) pop.ObjV = f # 把求得的目标函数值赋值给种群pop的ObjV if __name__ == "__main__": """================================实例化问题对象=============================""" problem = DTLZ1(3) # 生成问题对象 """==================================种群设置================================""" Encoding = 'RI' # 编码方式 NIND = 91 # 种群规模 Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器 population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化) """================================算法参数设置===============================""" myAlgorithm = ea.moea_NSGA3_templet(problem, population) # 实例化一个算法模板对象 myAlgorithm.MAXGEN = 500 # 最大进化代数 myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制过程动画) """===========================调用算法模板进行种群进化=========================== 调用run执行算法模板,得到帕累托最优解集NDSet。NDSet是一个种群类Population的对象。 NDSet.ObjV为最优解个体的目标函数值;NDSet.Phen为对应的决策变量值。 详见Population.py中关于种群类的定义。 """ NDSet = myAlgorithm.run() # 执行算法模板,得到非支配种群 # 输出 print('用时:%f 秒'%(myAlgorithm.passTime)) 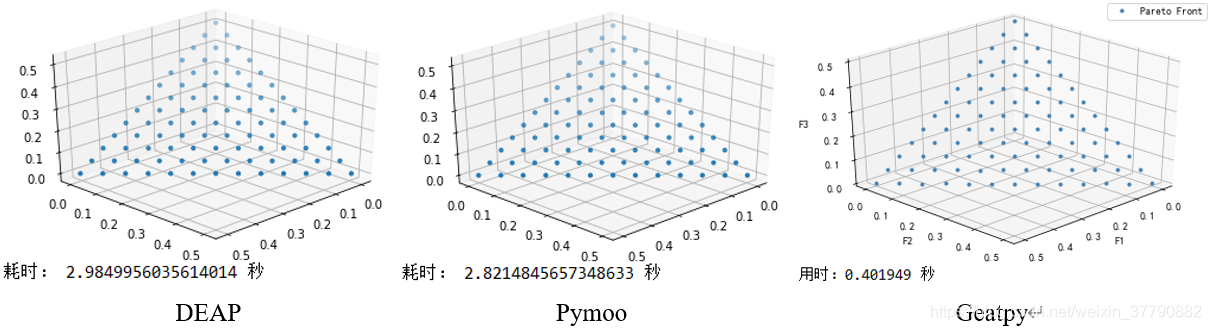
3.3 用MOEA/D 优化 ZDT1
from pymoo.algorithms.moead import MOEAD from pymoo.factory import get_problem, get_reference_directions from pymoo.optimize import minimize import matplotlib.pyplot as plt import time problem = get_problem("ZDT1") algorithm = MOEAD( get_reference_directions("das-dennis", 2, n_partitions=40), n_neighbors=40, decomposition="tchebi", prob_neighbor_mating=1 ) start = time.time() res = minimize(problem, algorithm, termination=('n_gen', 300)) end = time.time() plt.scatter(res.F[:, 0], res.F[:, 1], marker="o", s=10) plt.grid(True) plt.show() print('耗时:', end - start, '秒')
# -*- coding: utf-8 -*- import numpy as np import geatpy as ea class ZDT1(ea.Problem): # 继承Problem父类 def __init__(self): name = 'ZDT1' # 初始化name(函数名称,可以随意设置) M = 2 # 初始化M(目标维数) maxormins = [1] * M # 初始化maxormins(目标最小最大化标记列表,1:最小化该目标;-1:最大化该目标) Dim = 30 # 初始化Dim(决策变量维数) varTypes = [0] * Dim # 初始化varTypes(决策变量的类型,0:实数;1:整数) lb = [0] * Dim # 决策变量下界 ub = [1] * Dim # 决策变量上界 lbin = [1] * Dim # 决策变量下边界(0表示不包含该变量的下边界,1表示包含) ubin = [1] * Dim # 决策变量上边界(0表示不包含该变量的上边界,1表示包含) # 调用父类构造方法完成实例化 ea.Problem.__init__(self, name, M, maxormins, Dim, varTypes, lb, ub, lbin, ubin) def aimFunc(self, pop): # 目标函数 Vars = pop.Phen # 得到决策变量矩阵 ObjV1 = Vars[:, 0] gx = 1 + 9 * np.sum(Vars[:, 1:], 1) / (self.Dim - 1) hx = 1 - np.sqrt(np.abs(ObjV1) / gx) # 取绝对值是为了避免浮点数精度异常带来的影响 ObjV2 = gx * hx pop.ObjV = np.array([ObjV1, ObjV2]).T # 把结果赋值给ObjV if __name__ == "__main__": """================================实例化问题对象=============================""" problem = ZDT1() # 生成问题对象 """==================================种群设置================================""" Encoding = 'RI' # 编码方式 NIND = 40 # 种群规模 Field = ea.crtfld(Encoding, problem.varTypes, problem.ranges, problem.borders) # 创建区域描述器 population = ea.Population(Encoding, Field, NIND) # 实例化种群对象(此时种群还没被初始化,仅仅是完成种群对象的实例化) """================================算法参数设置===============================""" myAlgorithm = ea.moea_MOEAD_templet(problem, population) # 实例化一个算法模板对象 myAlgorithm.Ps = 1.0 # (Probability of Selection)表示进化时有多大的概率只从邻域中选择个体参与进化 myAlgorithm.MAXGEN = 300 # 最大进化代数 myAlgorithm.drawing = 1 # 设置绘图方式(0:不绘图;1:绘制结果图;2:绘制过程动画) """===========================调用算法模板进行种群进化=========================== 调用run执行算法模板,得到帕累托最优解集NDSet。NDSet是一个种群类Population的对象。 NDSet.ObjV为最优解个体的目标函数值;NDSet.Phen为对应的决策变量值。 详见Population.py中关于种群类的定义。 """ NDSet = myAlgorithm.run() # 执行算法模板,得到非支配种群 print('用时:%f 秒'%(myAlgorithm.passTime))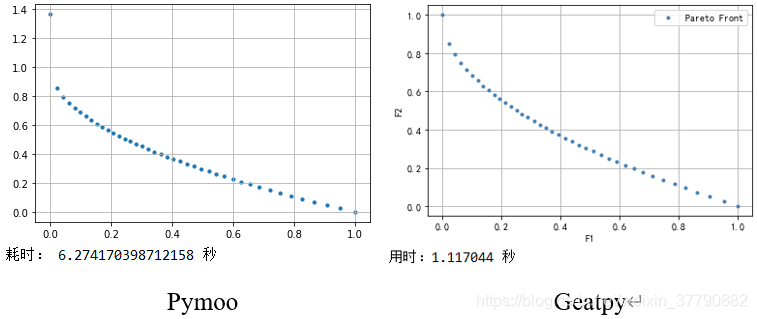
3.3 更多的比较
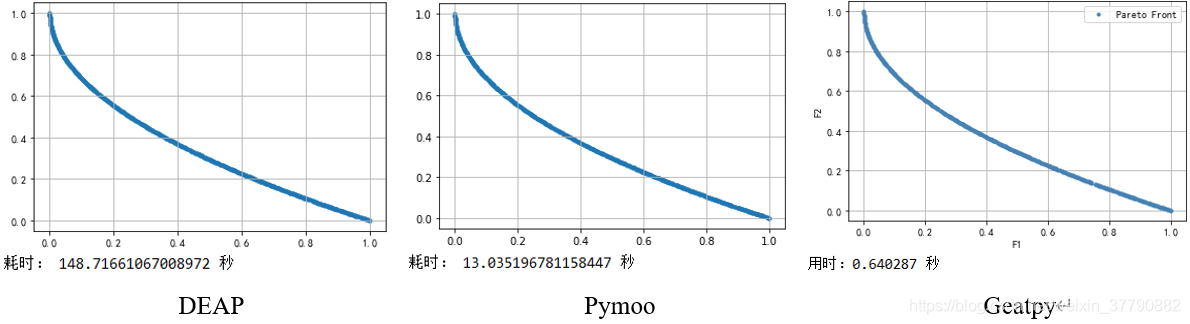
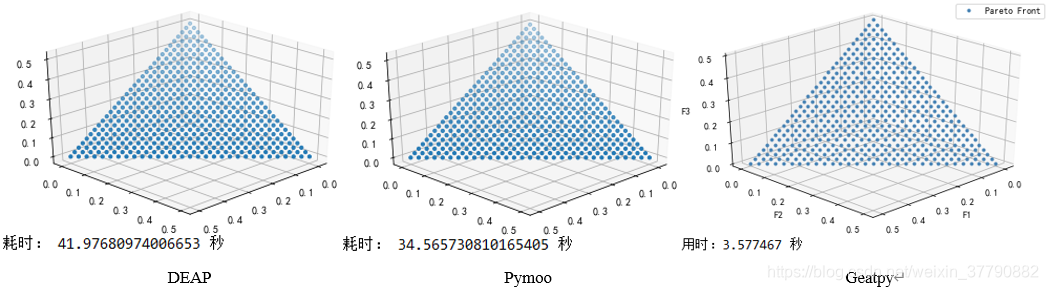
总结
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)