题目

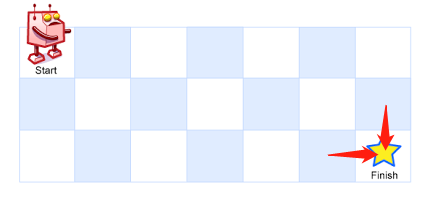
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

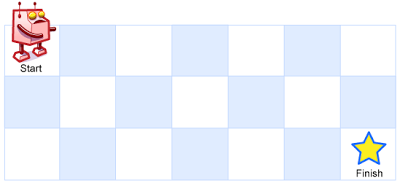
例如，上图是一个7 x 3 的网格。有多少可能的路径？

示例 1:

输入: m = 3, n = 2 输出: 3 解释: 从左上角开始，总共有 3 条路径可以到达右下角。 1. 向右 -> 向右 -> 向下 2. 向右 -> 向下 -> 向右 3. 向下 -> 向右 -> 向右 

示例 2:

输入: m = 7, n = 3 输出: 28 

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10 ^ 9

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-paths

思路

这个题目和爬楼梯问题很像。

很容易想出递归解法。机器人每次只能向下或者向右移动一步，网格右下角记为终点，到达终点有两种方法： 从终点位置上面往下走一步到达；从左边往右走一步到达。

所以只要用反向的思维就可以写出递归代码了。注意这是一个n行m列的网格。

代码

递归

class Solution(object): def unique(self, m, n): # 如果到达了起点，就是一种解法 if m == 0 and n == 0: return 1          ways = 0 # 如果可以向左回退一步 if m >= 1:             ways = self.unique(m - 1, n) # 如果可以向上回退一步 if n >= 1:             ways += self.unique(m, n - 1) return ways       def uniquePaths(self, m, n): """         :type m: int         :type n: int         :rtype: int         """ # 终点是m-1,n-1 return self.unique(m-1,n-1)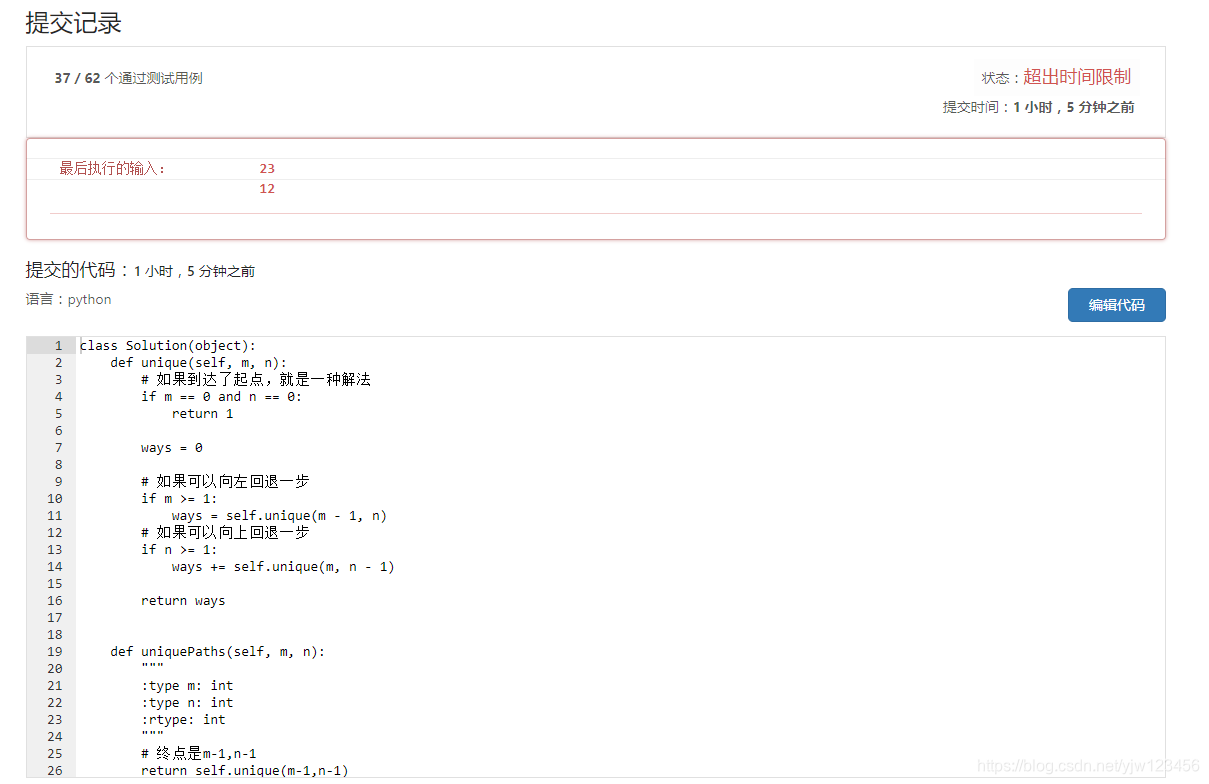 

虽然思路是对的，但是递归的方式是比较低效的，这里导致了计算超时。参阅LeetCode刷题之动态规划思想，我们可以将其改成记忆化搜索的方式，解决重叠子问题。

记忆化搜索

dp = {(0,0) : 1} #起点 class Solution(object): def unique(self, m, n): if (m,n) not in dp:             ways = 0 # 如果可以向左回退一步 if m >= 1:                 ways = self.unique(m - 1, n) # 如果可以向上回退一步 if n >= 1:                 ways += self.unique(m, n - 1)              dp[(m,n)] = ways         return dp[(m,n)] def uniquePaths(self, m, n): """         :type m: int         :type n: int         :rtype: int         """ # 终点是m-1,n-1 return self.unique(m-1,n-1)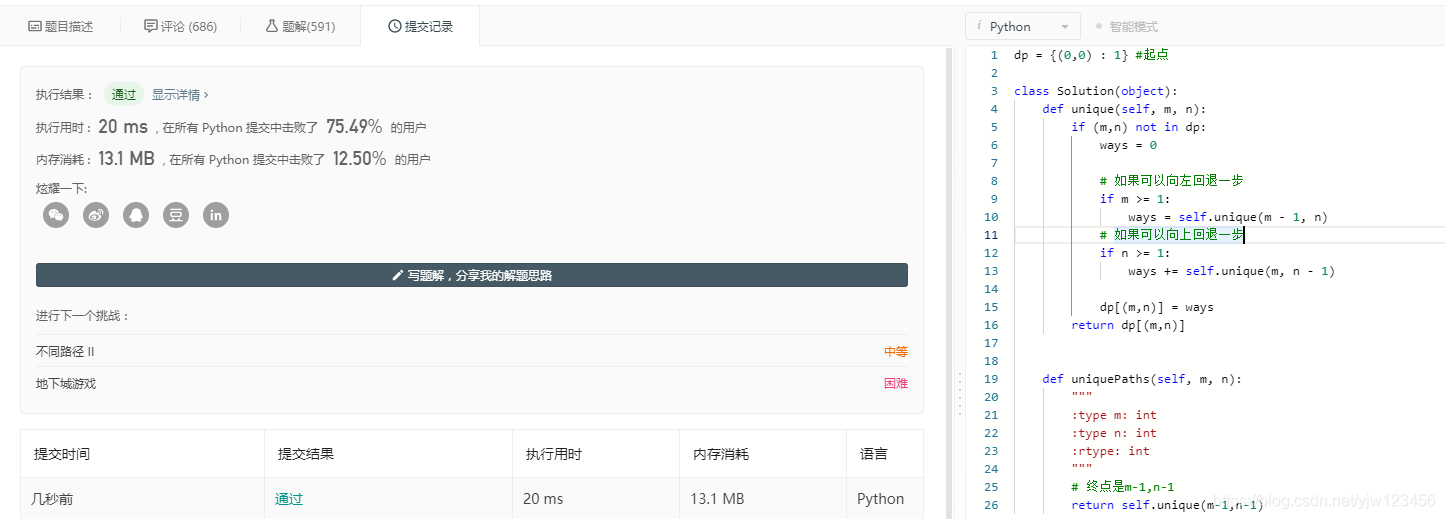 

动态规划

动态规划的解法也很简单，从起点开始考虑。dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 这句代码表示要达到第[i][j]个格子，可以有它的左边那么格子或上面那个格子达到。

我们只要处理好边界值，整个代码就很清爽。这点先处理边界值的思想也体现在了64. 最小路径和问题里面。

class Solution(object): def uniquePaths(self, m, n): # n行 m 列的列表          外层不能使用*，否则会浅拷贝内层         dp = [[0] * m for _ in range(n)] # 先设定好边界值 for i in range(0, n):             dp[i][0] = 1 for j in range(1, m):             dp[0][j] = 1 for i in range(1, n): for j in range(1, m): # dp[i][j] = 左边一步加上面一步的结果                 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] return dp[-1][-1] 

刷到了8ms。