并查集的介绍及简单应用—蓝桥杯真题：合根植物数据结构与算法CyrilKI的博客-

先简单介绍一下并查集：

在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。
并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

简单来说，就是：N个元素分布在若干个互不相交的集合中，需要进行以下三个操作：
1、合并两个集合。
2、查询一个元素在哪个集合里面。
3、查询两个元素是否属于同一个集合。
最典型的应用就是判断亲戚关系，给定n,一共n个人，再给定m组亲戚关系，最后让你判断任意两个人是否是亲戚关系。若a与b是亲戚关系，b与c是亲戚关系，那么很显然a,b,c三人互为亲戚关系，应该合并。

用并查集处理问题的过程中有几个重要的函数：
1、获得一个结点的根结点，若两个结点的根结点相同，那么两个结点就可以合并到一起。

int get_root(int a) { //求根节点  if(par[a]!=a) {   par[a]=get_root(par[a]); } return par[a]; } 

所有结点的根结点最开始都是自己，因为每个结点合并前都是单独存在的。查询这里用了递归的思想，实际上就是路径压缩。
2、查询两个结点是否属于同一个集合，只需要获取两个结点的根结点，若二者根结点相同，就属于同一个集合。

bool query(int a,int b) { return get_root(a)==get_root(b); } 

3、合并操作，若要合并两个结点，直接令一个结点的根结点的父结点为另一个结点的根结点即可：par[get_root(a)]=get_root(b)；

void merge(int a,int b) {      par[get_root(a)]=get_root(b); } 

4、若要计算每个集合有多少人，就需要改写merge()函数：

void merge(int a,int b) { int p1=get_root(a); int p2=get_root(b); if(p1==p2) { return ; }else {   total[p1]+=toatl[p2];   par[p2]=p1; } } 

下面回到蓝桥杯合根植物这道题：
问题描述：

w星球的一个种植园，被分成 m * n 个小格子（东西方向m行，南北方向n列）。每个格子里种了一株合根植物。
　　这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。
　　如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

输入格式：

第一行，两个整数m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。
接下来一行，一个整数k，表示下面还有k行数据(0<k<100000)
接下来k行，第行两个整数a，b，表示编号为a的小格子和编号为b的小格子合根了。格子的编号一行一行，从上到下，从左到右编号。比如：5* 4 的小格子，编号： 　　
1 2 3 4 　　
5 6 7 8 　　
9 10 11 12 　　
13 14 15 16 　　
17 18 19 20

样例输入：
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
样例输出：
5
样例解释：

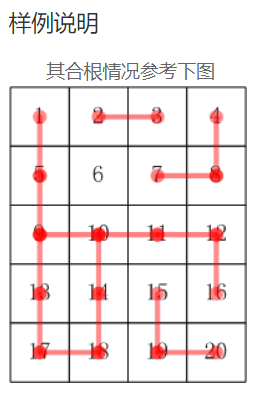
思路分析：就是简单的并查集应用：先合并有关系的结点，最后输出一个有几个不同的集合，其实就是输出最后还有几个根结点。

#include<bits/stdc++.h> using namespace std; int par[1000*1000]; int get_root(int a) { //求根节点  if(par[a]!=a) {   par[a]=get_root(par[a]); } return par[a]; } void merge(int a,int b) {  par[get_root(b)]=get_root(a); } int main() {  set <int> s; int m,n,k; int x,y;  cin>>m>>n;  cin>>k; for(int i=0;i<m*n;i++) {   par[i]=i; //刚开始构成m*n个集合，每个元素的父节点都是自己  } for(int i=0;i<k;i++) {   cin>>x>>y; merge(x,y); //合并x,y,最终答案就是合并后有多少个集合，即有几个不同的根节点  } for(int i=0;i<m*n;i++) {   s.insert(get_root(i)); }  cout<<s.size(); return 0; }