计算机系统基础学习笔记(4)-Cache友好代码c/c++BeiXi's Blog-

程序的性能指执行程序所用的时间，显然程序的性能与程序执行时访问指令和数据所用的时间有很大关系，而指令和数据的访问时间与相应的 Cache 命中率、命中时间和和缺失损失有关。对于给定的计算机系统而言，命中时间和缺失损失是确定的。因此，指令和数据的访存时间主要由 Cache 命中率决定，而 Cache 的命中率则主要由程序的空间局部性和时间局部性决定。

Cache友好代码

下面我们来介绍如何编写一段Cache友好代码，一段Cache友好代码往往运行速度较快。但我们需要注意以下两点：

1. 尽可能多的重复使用一个数据（时间局限性）【如果我们需要在某个任务多次使用一个数据时，应该尽可能的一次性使用完，利用了数据的局部性特点】
2. 尽可能跨距为1的访问数据（空间局部性）【在访问一个数据时，应该依次的访问数组元素，不要跳着访问，利用了数据的空间局限性】

当我们访问一个内存地址单元时会将同一块的的数据同时从内存读入到Cache,这样如果我们继续访问附近的数据，那它就已经位于Cache中，访问速度就会很快。

矩阵相乘

我们知道，两个矩阵相乘，可以通过三层循环来实现，可以使用临时变量来累加最内层的中间结果。以矩阵A,矩阵B来给大家介绍：

for(i=0;i<n;i++){ for(j=0;j<n;j++){ for(k=0;k<n;k++){     C[i+j*n]+=A[i+k*n]*B[k+j*n]; } } } 

事实上，循环的顺序对最终结果并没有影响。因此可以有6种循环顺序：ijk, ikj, jik, jki, kij, kji 等。接下来我们以math.c这样一个简单的C语言程序来分别了解这六种顺序的运行时间。

#include <stdio.h> #include <stdlib.h> #include <sys/time.h> #include <time.h> //ijk void multMat1(int n, float *A,float *B,float *C) { int i,j,k; for(i=0;i<n;i++){ for(j=0;j<n;j++) { for(k=0;k<n;k++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } //ikj void multMat2(int n, float *A,float *B,float *C) { int i,j,k; for(i=0;i<n;i++){ for(k=0;k<n;k++) { for(j=0;j<n;j++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } //jik void multMat3(int n, float *A,float *B,float *C) { int i,j,k; for(j=0;j<n;j++){ for(i=0;i<n;i++) { for(k=0;k<n;k++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } //jki void multMat4(int n, float *A,float *B,float *C) { int i,j,k; for(j=0;j<n;j++){ for(k=0;k<n;k++) { for(i=0;i<n;i++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } //kij void multMat5(int n, float *A,float *B,float *C) { int i,j,k; for(k=0;k<n;k++){ for(i=0;i<n;i++) { for(j=0;j<n;j++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } //kji void multMat6(int n, float *A,float *B,float *C) { int i,j,k; for(k=0;k<n;k++){ for(j=0;j<n;j++) { for(i=0;i<n;i++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } } } int main(int argc, char **argv) { int nmax = 1024,i,n; //函数指针数组，存放6个函数指针，分别对应着按照6种不同的顺序执行矩阵相乘的函数 void (*orderings[])(int,float *,float *,float *) = {&multMat1,&multMat2,&multMat2,&multMat3,&multMat4,&multMat5,&multMat6}; char *names[] = {"ijk","ikj","jik","jki","kij","kji"}; //声明了三个浮点类型指针变量A,B,C float *A = (float *)malloc(nmax*nmax * sizeof(float)); float *B = (float *)malloc(nmax*nmax * sizeof(float)); float *C = (float *)malloc(nmax*nmax * sizeof(float)); struct timeval start,end; for(i=0;i<nmax*nmax;i++)A[i] = drand48()*2-1; for(i=0;i<nmax*nmax;i++)B[i] = drand48()*2-1; for(i=0;i<nmax*nmax;i++)C[i] = 0; for(i=0;i<6;i++) { gettimeofday(&start,NULL); (*orderings[i])(nmax,A,B,C); gettimeofday(&end,NULL); double seconds = (end.tv_sec - start.tv_sec)+1.0e-6 * (end.tv_usec - start.tv_usec); printf("%s:tn = %d,%.3f sn",names[i],nmax,seconds); } return 0; } 

可以看出六种循环顺序只是循环顺序变化了，最内层的计算并没有改变。
利用gcc命令进行编译并且执行

gcc -o0 -m32 -g math.c -o math ./math 

执行结果如下：

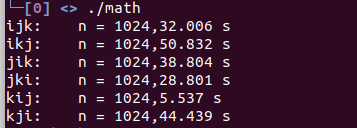
通过执行结果可以体现Cache算法的效率的影响是非常的大。

矩阵的存储——空间局部性

在计算机内部，矩阵中的数据按顺序存储，访问相邻的数据时，应当尽可能地遵从空间局部性和时间局部性。其中在C语言中，二维矩阵采取地是行优先存储，也就是依次顺序地存储每一行的数据。

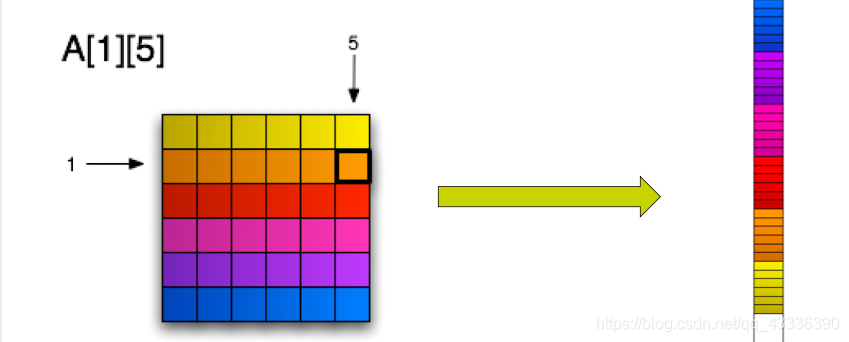
接下来我们分别讨论一下在这6种顺序下矩阵相乘算法的空间和时间局部性。

矩阵相乘——ijk

for(i=0;i<n;i++){ for(j=0;j<n;j++) { for(k=0;k<n;k++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } }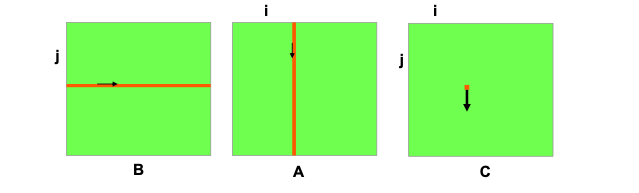 

矩阵B中第j行与矩阵A中第i列中对应的元素相乘并累加，得到矩阵C中的第j行第i列元素的值，可以看出矩阵A的访问不是顺序的，而是跨越了一行的数据。如果矩阵过大，Cache放不下整个矩阵的数据，矩阵A的访问就会变慢。

矩阵相乘——ikj

for(i=0;i<n;i++){ for(k=0;k<n;k++) { for(j=0;j<n;j++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } }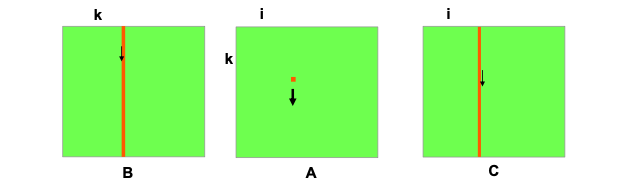 

矩阵B中第k列，与矩阵A的第k行第i列的中的元素分别相乘得到矩阵C中的第i列元素的值，可以看到矩阵B和矩阵C的访问都不是顺序的，因此速度就最慢。

矩阵相乘——jik

for(j=0;j<n;j++){ for(i=0;i<n;i++) { for(k=0;k<n;k++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } }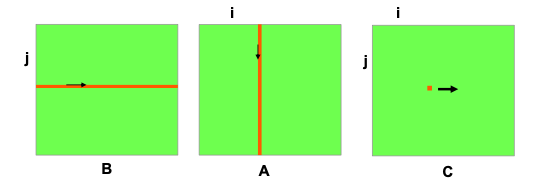 

矩阵B中第j行与矩阵A的第i列中对应的元素相乘并累加得到矩阵C中的第j行第i列元素的值。矩阵A的访问不是顺序的，而是跨越了一行，所以它的访问速度也不快。

矩阵相乘——jki

for(j=0;j<n;j++){ for(k=0;k<n;k++) { for(i=0;i<n;i++) {     C[i+j*n] += A[i+k*n]*B[k+j*n]; } } }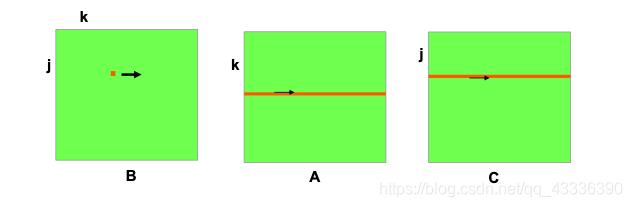 

矩阵B中第j行第k列元素分别与矩阵A的第k行元素相乘，得到矩阵C中的第j行元素的部分值。可以看到矩阵A,矩阵C的访问顺序是顺序的，对Cache的利用最好，因此jki的运行速度最快。

剩下的两个顺序，分析方法和前面四个相似，就不一一分析了。。。。。。

时间局部性

在这之前的的乘法都是考虑的是空间局部性问题，其实矩阵相乘还有时间局部性问题。以ijk顺序计算为例：

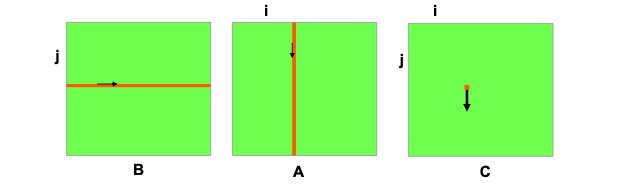
矩阵B中的一行依次与矩阵A的每一列相乘，并累加，得到矩阵C中的一个元素值。矩阵B的时间局部性很好，每一行读取后，与矩阵A中所有的列依次相乘，当它计算完以后，就不会再去需要使用该行的数据。但是矩阵A的时间局部性就很差，矩阵A的某一列会在不同的时间被多次读取使用。

分块矩阵相乘

为了解决矩阵A的时间局部性就很差的问题，我们继续介绍一种常用的算法——分块算法，可以部分的减缓这一个问题。

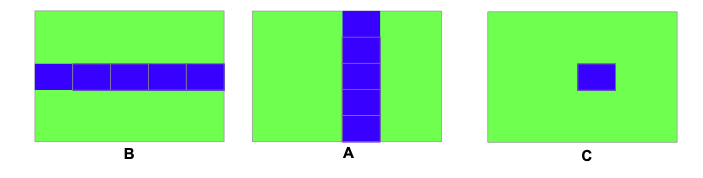
如上图所示，我们不再以行和列为单位来进行计算，将矩阵分成同样大小的若干块，以块为单位进行计算，提升矩阵A的时间局部性。

仍然以一个简单的C语言程序来验证分块策略对于程序的影响。

#include <stdio.h> #include <stdlib.h> #include <sys/time.h> #include <time.h> void multMat(int n, float *A,float *B,float *C,int blocksize) { int i,j,k,b_i,b_j,b_k; register float tem =0; int block_num = n/blocksize; printf("block_num=%dn",block_num); for(b_i=0;b_i<block_num;b_i++){ for(b_j=0;b_j<block_num;b_j++){ for(b_k=0;b_k<block_num;b_k++){ for(i=0;i<blocksize;i++){ for(j=0;j<blocksize;j++){       tem=0; for(k=0;k<blocksize;k++){        tem +=A[(b_i*blocksize+i)*n+b_k*blocksize+k]*B[(b_k*blocksize+k)*n+b_j*blocksize+j];        C[(b_i*blocksize+i)*n+b_j*blocksize+j] += tem; } } } } } } } void multMat3(int n, float *A,float *B,float *C) { int i,j,k; register float tem =0; for(i=0;i<n;i++){ for(j=0;j<n;j++) {    tem=0; for(k=0;k<n;k++){     tem += A[i*n+k]*B[k*n+j]; }    C[i*n+j]=tem; } } } int main(int argc, char **argv) { int nmax = 2048,i,j; int blocksize=16; float tem = 0; double seconds; //声明了四个2048*2048的大小的矩阵，矩阵元素为单精度浮点数。A和B为初始矩阵。 float *A = (float *)malloc(nmax*nmax * sizeof(float)); float *B = (float *)malloc(nmax*nmax * sizeof(float)); float *C = (float *)malloc(nmax*nmax * sizeof(float)); float *D = (float *)malloc(nmax*nmax * sizeof(float)); struct timeval start,end; for(i=0;i<nmax*nmax;i++)A[i] = drand48()*2-1;//对矩阵A进行赋值 for(i=0;i<nmax*nmax;i++)B[i] = drand48()*2-1;//对矩阵B进行赋值 for(i=0;i<nmax*nmax;i++)C[i] = 0;//存放未分块相乘的结果 for(i=0;i<nmax*nmax;i++)D[i] = 0;//存放分块相乘的结果 gettimeofday(&start,NULL); multMat3(nmax, A, B, D); gettimeofday(&end,NULL);    seconds = (end.tv_sec - start.tv_sec)+1.0e-6 * (end.tv_usec - start.tv_usec); printf("n= %d,time = %.3f sn",nmax,seconds); gettimeofday(&start,NULL); multMat(nmax, A, B, C,blocksize); gettimeofday(&end,NULL);    seconds = (end.tv_sec - start.tv_sec)+1.0e-6 * (end.tv_usec - start.tv_usec); printf("n= %d,blocksize = %d,time = %.3f sn",nmax,blocksize,seconds); //统计两个结果之差 for(i=0;i<nmax;i++) { for(j=0;j<nmax;j++){    tem+=(C[i*nmax+j]-D[i*nmax+j])*(C[i*nmax+j]-D[i*nmax+j]); } } printf("error=%.4fn",tem); free(A); free(B); free(C); free(D); return 0; } 

该代码首先声明了四个2048*2048的大小的矩阵，矩阵元素为单精度浮点数。其中A和B为初始矩阵。矩阵C存放未分块相乘的结果，矩阵存放分块相乘的结果。在程序的末尾对这两个结果的差作出了统计输出，对比判断结果的正确性。在具体的矩阵分块算法实现时，利用了6层循环，分别是block上的三层循环和block内的三层循环。

运行结果可以看出，在分块的作用下时间耗费上，程序性能有了大幅的提升。也可以改变block的大小，其结果也是类似的，而且在上述执行过程中，矩阵的计算结果也是一样的。

我们可以通过编程来充分利用cache性能，但是我们需要同时考虑数据的组织形式和数据的访问形式，此外，可以使用分块处理的方式获得空间局部性更好的方法。获得最佳Cache性能是与平台相关的，比如，Cache的大小，Cache行大小，以及映射策略。比较通用的法则当然是工作集越小越好，访问跨距越小越好。

前面的路布满荆棘，我有过迟疑，却从未后退。一无所有，就是拼的理由!

以上就是本次给大家的计算机系统基础学习笔记-Cache友好代码，希望各位小伙伴能有所收获，如果有问题的地方，可以在评论区留言哟，当然觉得还不错的小伙伴，就留下你的金赞吧，你的支持就是我前进的动力哇。