引言

本文是吴恩达深度学习第一课：神经网络与深度学习的笔记。神经网络与深度学习主要讨论了如何建立神经网络(包括一个深度神经网络)、以及如何训练这个网络。

第一课有以下四个部分，本文是第四部分。

1. 深度学习概论
2. 神经网络基础
3. 浅层神经网络
4. 深层神经网络

深层神经网络

我们已经了解逻辑回归和单隐层神经网络了。
下面是2个和5个隐藏层的例子：

我们知道逻辑回归可以看成一个浅层模型，而上图5隐藏层的神经网络明显要深的多。

有些问题只有深层神经网络才能处理，具体要多少层，也是一个可以探索的超参数。

下面看下描述深层神经网络的符号。

这是一个四层神经网络，输入层不计。每层的神经元数分别是5，5，3，1。

• 我们用大写的
  $L$

  L表示神经网络的层数，这里
  $L=4$

  L=4；

• 用
  $n^{[l]}$

  n[l]表示
  $l$

  l层上的神经元数量(输入层可以看出第
  $0$

  0层,
  $n^{[0]} = n_x = 3$

  n[0]=nx​=3)；

  • 特别地，最后一层可以用
    $L$

    L来表示，有
    $n^{[L]}=1$

    n[L]=1。

• 用
  $a^{[l]} = g^{[l]}(z^{[l]})$

  a[l]=g[l](z[l])表示每层的激活函数值，最后一层激活值
  $a^{[L]}=hat y$

  a[L]=y^​；

• 用
  $W^{[l]}$

  W[l]表示
  $l$

  l层的权值,
  $b^{[l]}$

  b[l]表示每层的偏置；

• 输入特征用
  $x$

  x表示，
  $x$

  x也可以说是
  $a^{[0]}$

  a[0]；

深层网络中的前向传播

先看下给定上面这样的神经网络，并有一个样本
$x$

x，如何计算第一层的激活值。

$x$

x:
$z^{[1]} = W^{[1]}a^{[0]} + b^{[1]}$

z[1]=W[1]a[0]+b[1] 这里的
$x$

x用
$a^{[0]}$

a[0]来表示。

$a^{[1]} = g^{[1]}(z^{[1]})$

a[1]=g[1](z[1])

那第二层呢

$z^{[2]} = W^{[2]}a^{[1]} + b^{[2]}$

z[2]=W[2]a[1]+b[2]

$a^{[2]} = g^{[2]}(z^{[2]})$

a[2]=g[2](z[2])

后面几层以此类推。我们来算下输出层：

$z^{[4]} = W^{[4]} a^{[3]} + b^{[4]}$

z[4]=W[4]a[3]+b[4]

$a^{[4]} = g^{[4]}(z^{[4]}) = hat y$

a[4]=g[4](z[4])=y^​

因此，基本规律就是：

$z^{[l]} = W^{[l]} a^{[l-1]} +b^{[4]}$

z[l]=W[l]a[l−1]+b[4]

$a^{[l]} = g^{[l]}(z^{[l]})$

a[l]=g[l](z[l])

上面是针对一个样本，如果多个样本，怎么向量化呢。

第一层。

$X$

X:
$Z^{[1]} = W^{[1]}A^{[0]} + b^{[1]}$

Z[1]=W[1]A[0]+b[1] 这里的
$X$

X用
$A^{[0]}$

A[0]来表示。

$A^{[1]} = g^{[1]}(Z^{[1]})$

A[1]=g[1](Z[1])

第二层

$Z^{[2]} = W^{[2]}A^{[1]} + b^{[2]}$

Z[2]=W[2]A[1]+b[2]

$A^{[2]} = g^{[2]}(Z^{[2]})$

A[2]=g[2](Z[2])

后面几层以此类推。我们来算下输出层：

$Z^{[4]} = W^{[4]} A^{[3]} + b^{[4]}$

Z[4]=W[4]A[3]+b[4]

$A^{[4]} = g^{[4]}(Z^{[4]}) = hat y$

A[4]=g[4](Z[4])=y^​

因此，基本规律就是：

$Z^{[l]} = W^{[l]} A^{[l-1]} +b^{[4]}$

Z[l]=W[l]A[l−1]+b[4]

$A^{[l]} = g^{[l]}(Z^{[l]})$

A[l]=g[l](Z[l])

看起来只要一个for l in range(1,L+1)循环就好了，这个循环是必须的哦，不能再向量化了。

在实现深层神经网络时，想要得到没有bug的程序，最好要仔细核对矩阵的维数。下面就来看一下。

核对矩阵的维数

我们有个这样的NN，我们知道

$z^{[1]} = W^{[1]} x + b^{[1]}$

z[1]=W[1]x+b[1]

我们来看下上面几个符号的维数。

$z^{[1]}$

z[1]是第一个隐藏层的激活值向量，第一个隐藏层的单元数
$n^{[1]}=3$

n[1]=3，所以它的维度是
$(3,1)$

(3,1)，也可以写成
$(n^{[1]},1)$

(n[1],1)。

$x$

x有2个输入特征，所以维度是
$(2,1)$

(2,1),也就是
$(n^{[0]},1)$

(n[0],1)。

我们需要
$W^{[1]}$

W[1] 乘以一个
$(n^{[0]},1)$

(n[0],1)的向量能得到
$(n^{[1]},1)$

(n[1],1)的向量，因此
$W^{[1]}$

W[1]的维度要是
$(n^{[1]},n^{[0]})$

(n[1],n[0])，这里是
$(3,2)$

(3,2)。
$W^{[l]}$

W[l] 就是对
$l$

l层的每个单元对每个输入都有1个权重，总共有
$n^{[l]}$

n[l]个单元，以及
$n^{[l-1]}$

n[l−1]个输入，即**(单元数，输入数)**。

总结起来，
$W^{[l]}$

W[l]的维度必须是
$(n^{[l]},n^{[l-1]})$

(n[l],n[l−1])。

比如
$W^{[2]}$

W[2]的维度是
$(5,3)$

(5,3)，即
$(n^{[2]},n^{[1]})$

(n[2],n[1])。

我们知道每个逻辑回归单元只有一个偏置，每层有
$n^{[l]}$

n[l]个单元，因此
$b^{[l]}$

b[l]的维度是
$(n^{[l]},1)$

(n[l],1)。

在实现反向传播时
$dW$

dW和
$db$

db的维度与
$W$

W和
$b$

b的维度是一样的。

再来看下
$z^{[l]}$

z[l]和
$a^{[l]}$

a[l]，因为
$z^{[l]} = g^{[l]}(a^{[l]})$

z[l]=g[l](a[l])，所以它们的维度是一样的。

我们再来看下向量化后的维度，哪怕向量化后，下面这几个参数的维度是一样的。

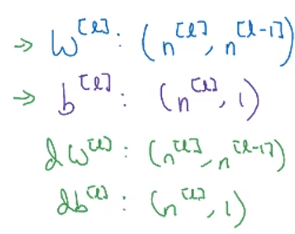
变化的是
$Z,A,X(=A^{[0]})$

Z,A,X(=A[0])的维度。

我们已经知道向量化之前上面的维度。

向量化后，

$Z^{[1]} = W^{[1]} X + b^{[1]}$

Z[1]=W[1]X+b[1]

$Z^{[1]}$

Z[1]是
$(Z^{[1](1)},Z^{[1](2)},cdots,Z^{[1](m)})$

(Z[1](1),Z[1](2),⋯,Z[1](m)) m个样本叠加到一起的结果。

所以
$Z^{[1]}$

Z[1]的维度是
$(n^{[1]},m)$

(n[1],m)。

$X$

X也是叠加后的结果，类似
$Z^{[1]}$

Z[1],
$X$

X的维度是
$(n^{[0]},m)$

(n[0],m)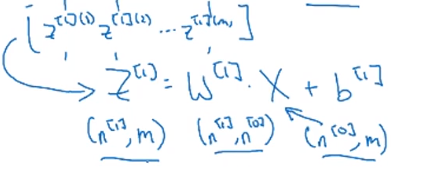

向上面所说的
$b^{[1]}$

b[1]的维度还是
$(n^{[1]},1)$

(n[1],1)，我们可以用python的广播直接相加。

向量化后
$Z^{[l]},A^{[l]}$

Z[l],A[l]的维度中的列变成了样本数。

为什么使用深层表示

我们先来看下深度神经网络在看下，假设你建立一个人脸识别系统，输入一张人脸图片后，(CNN)隐藏层中的第一层，可以看成是边缘检测。

上图中的小方块就代表一个隐藏神经元，它们会检测有没有出现这种边缘的图像。

如果把第一层中的边缘放到一起，可能就形成脸部的不同特征。可能有些单元在检测左眼部分，有些在检测鼻子部分。

最后把它们放到一起，就可以检测不同的人脸了。

通常我们可以把这个神经网络前面几层看成是探测边缘的函数，之后把后面几层结合在一起，那么总体上就可以学习更加复杂的函数。

因此，这需要神经网络有一定的深度。深度神经网络其实就是很多隐藏层的神经网络。

当遇到新问题时，建议先从逻辑回归开始，然后尝试一到两层的神经网络，把隐藏层数量当成超参数取寻找比较合适的层数。

搭建深度神经网络

我们先来关注第
$l$

l层的。

正向传播：上面是如何从输入
$a^{[l-1]}$

a[l−1]到输出
$a^{[l]}$

a[l]的相关步骤，此时需要把
$z^{[l]}$

z[l]的值缓存起来，这样对后面的正向传播和反向传播都很有用。

反向传播：反向传播的输入是
$da^{[l]}$

da[l]，输出是
$da^{[l-1]}$

da[l−1]。

总结起来，在第
$l$

l层，我们会有正向函数来计算正向传播

然后用作反向传播的反向函数是

如果已经实现了这两个函数，那么神经网络的计算过程会是下面这样的：

首先是正向传播，从
$a^{[0]}$

a[0]到
$a^{[L]} = hat y$

a[L]=y^​需要缓存所有的
$z^{[l]}$

z[l],以便反向传播时使用。

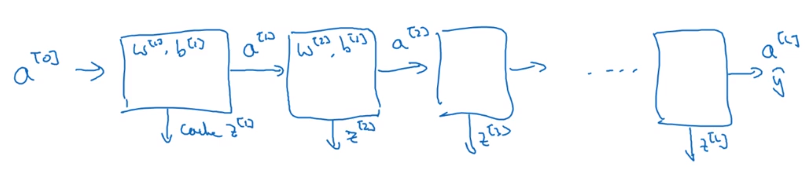
然后是反向传播

所以神经网络的训练，从
$a^{[0]}(x)$

a[0](x)开始，然后经过一系列正向传播得到输出
$hat y$

y^​，然后再实现反向传播，更新每层的参数。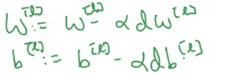

前向和反向传播

本节我们看下具体如何实现前向和反向传播。

在前向传递过程中最好也缓存
$W^{[l]},b^{[l]}$

W[l],b[l]，这些都在反向传播中用得到。上图右边就是向量化后的公式。

下面看下反向传播的步骤。

上面的公式其实就是上篇文章中反向传播相关的公式。只需要四步，加上对每层的(反向)循环，就能写出反向传播的代码。

总结一下，就是给定输入
$X$

X，如果用ReLU作为激活函数的话，经过几层隐藏层，最后用sigmoid作为输出层的激活函数，得到输出，然后需要计算出成本函数。

接着就可以反向迭代，先是计算
$da^{[L]},dW^{[L]},db^{[L]}$

da[L],dW[L],db[L]，然后反向传播。

下面我们来看下之前一直说的超参数。

参数与超参数

我们已经知道了参数是
$W,b$

W,b这种，那超参数是什么呢

超参数就是输入到学习算法的参数，比如学习率在神经网络中还有隐藏层的层数，每个隐藏层的隐藏单元数，还可以选择激活函数。

这些会控制我们得到的参数
$W,b$

W,b，因此它们叫超参数。

应用深度学习是非常依据经验的，可能你知道通常什么样的学习率比较好。如果不知道的话， 你就需要不停的尝试。

比如先尝试了一个比较大的学习率，结果随着迭代次数的增加，损失值反而增加；此时你就需要减小学习率，不停的尝试，最终选择一个比较好的学习率。

其他超参数的选择也是一样的。

要注意的是，在开发的过程中，可能学习率(或其他超参数)的最优数值是会变化的，因为电脑的CPU或GPU或者数据可能会变化很大。

参考

(推荐网易云课堂，可以免费看并且还有课堂笔记。)

1. 吴恩达深度学习