前言

在业界有几种不同的流派（业界建立逻辑回归）

• 直接用原始变量进行回归（模型粗糙并不能生成评分卡）
• 从原始数据生成0/1的虚拟变量（dummy variable）进行回归（FICO用的较多，已不是主流）
• 从原始数据生成woe（weight of evidence）进行回归

1.逻辑回归原理

1.1 求解方式

预测函数(线性回归模型上加了sigmoid函数)：
$h_theta(x)=frac{1}{1+e^{-theta x}} qquad 其中theta x=theta _0+theta _1x_1+theta _2x_2+…+theta _nx_n$

hθ​(x)=1+e−θx1​其中θx=θ0​+θ1​x1​+θ2​x2​+...+θn​xn​
对于二分类：

$begin{cases} p(y=1|x,theta)=h_theta(x)\ p(y=0|x,theta)=1-h_theta(x)\ end{cases}$

{p(y=1∣x,θ)=hθ​(x)p(y=0∣x,θ)=1−hθ​(x)​
将其合并得到：

$p(y|x,theta)=h_theta(x)^y(1-h_theta(x))^{(1-y)}$

p(y∣x,θ)=hθ​(x)y(1−hθ​(x))(1−y)
利用极大似然估计得到（MLE）：

$L_{(theta)}=prod_{i=1}^np(y_i|x_i,theta)=prod_{i=1}^nh_theta(x_i)^{y_i}(1-h_theta(x_i))^{(1-y_i)}$

L(θ)​=i=1∏n​p(yi​∣xi​,θ)=i=1∏n​hθ​(xi​)yi​(1−hθ​(xi​))(1−yi​)
两边同时取log：

$logL_{(theta)}=sum_{i=1}^m[y_ilogh_theta(x_i)+(1-y_i)log(1-h_theta(x_i))]$

logL(θ)​=i=1∑m​[yi​loghθ​(xi​)+(1−yi​)log(1−hθ​(xi​))]
对于
$logL_{(theta)}$

logL(θ)​求最优解即是求最大值(MLE)，为了用梯度下降的算法对
$logL_{(theta)}$

logL(θ)​取负数，即
$-logL_{(theta)}$

−logL(θ)​最小值也就是
$logL_{(theta)}$

logL(θ)​的最大值：

$J(w)=-frac{1}{m}logL_{(theta)}=-frac{1}{m}sum_{i=1}^m[y_ilogh_theta(x_i)+(1-y_i)log(1-h_theta(x_i))]$

J(w)=−m1​logL(θ)​=−m1​i=1∑m​[yi​loghθ​(xi​)+(1−yi​)log(1−hθ​(xi​))]
根据梯度下降的求解可得
$theta_j$

θj​的更新方式：

$theta_j:=theta_j-alphafrac{1}{m}sum_{i=1}^m(h_theta(x_i)-y_i)x_i^j$

θj​:=θj​−αm1​i=1∑m​(hθ​(xi​)−yi​)xij​

1.2 逻辑回归为什么用sigmoid并且转化后的输出即为1的概率

逻辑回归的假设是y服从伯努利分布(E(X)=p，D(X)=p(1-p)),可以得出概率函数：

$f(x|p)=p^x(1-p)^{1-x}=exp(eta*x+ln(1+e^eta))implieseta=ln(frac{p}{1-p})满足条件1$

f(x∣p)=px(1−p)1−x=exp(η∗x+ln(1+eη))⟹η=ln(1−pp​)满足条件1

$eta=xbeta implies(结合eta=ln(frac{p}{1-p})) implies E(Y)=p=g^{-1}(eta)=frac{1}{1+e^{-eta}}满足条件2、3$

η=xβ⟹(结合η=ln(1−pp​))⟹E(Y)=p=g−1(η)=1+e−η1​满足条件2、3
在伯努利分布中E(Y)=p表示的就是1的概率

2.逻辑回归到评分卡

2.1 woe及IV

woe的计算公式：

$WOE_i=lnfrac{p(y_{i1})}{p(y_{i0})}=lnfrac{frac{B_i}{B}}{frac{G_i}{G}}(p(y_{i1})为i区间坏样本占总体坏样本比例，p(y_{i0})为i区间好样本占总体好样本比例，越大这个分组坏样本可能性越大)$

WOEi​=lnp(yi0​)p(yi1​)​=lnGGi​​BBi​​​(p(yi1​)为i区间坏样本占总体坏样本比例，p(yi0​)为i区间好样本占总体好样本比例，越大这个分组坏样本可能性越大)
IV的计算公式：

$IV_i=(p(y_{i1})-p(y_{i0}))*WOE_i(WOE的加权求和。IV越大，区分度越大，价值越大)$

IVi​=(p(yi1​)−p(yi0​))∗WOEi​(WOE的加权求和。IV越大，区分度越大，价值越大)

2.2 逻辑回归到评分卡

$ln(odds)=ln(frac{p}{1-p})=theta _0+theta _1x_1+theta _2x_2+…+theta _nx_n(其中x一般是woe编码后的值，也可以是原始数据，输出即为1的概率)$

ln(odds)=ln(1−pp​)=θ0​+θ1​x1​+θ2​x2​+...+θn​xn​(其中x一般是woe编码后的值，也可以是原始数据，输出即为1的概率)
以上给的是概率，有时候还需要将概率以分数形式输出，类似于蚂蚁分。具体如下：

$Score_总=A+B*ln(odds)$

Score总​=A+B∗ln(odds)
转换步骤：
1、设定
$odds=theta _0$

odds=θ0​时的分数
$P_0$

P0​
2、设定
$odds$

odds每增加一倍时，增加分数为
$PDO$

PDO
3、当
$odds=theta _0$

odds=θ0​时的分数
$P_0$

P0​，
$odds=2theta _0$

odds=2θ0​分数为
$P_0+PDO$

P0​+PDO

$begin{cases} p_0=A+Bln(theta _0)\ p_0+PDO=A+Bln(2theta _0)\ end{cases}$

{p0​=A+Bln(θ0​)p0​+PDO=A+Bln(2θ0​)​

$impliesbegin{cases} B=frac{PDO}{ln(2)}\ A=P_0-Bln(theta _0)\ end{cases}$

⟹{B=ln(2)PDO​A=P0​−Bln(θ0​)​

2.3 评分卡的开发流程

具体可参考建模流程https://blog.csdn.net/weixin_41851055/article/details/106194063

• 一个好的评分卡，样本分数平滑且接近正太分布，建模样本与验证样本保持一致
• 
  $log(odds)$

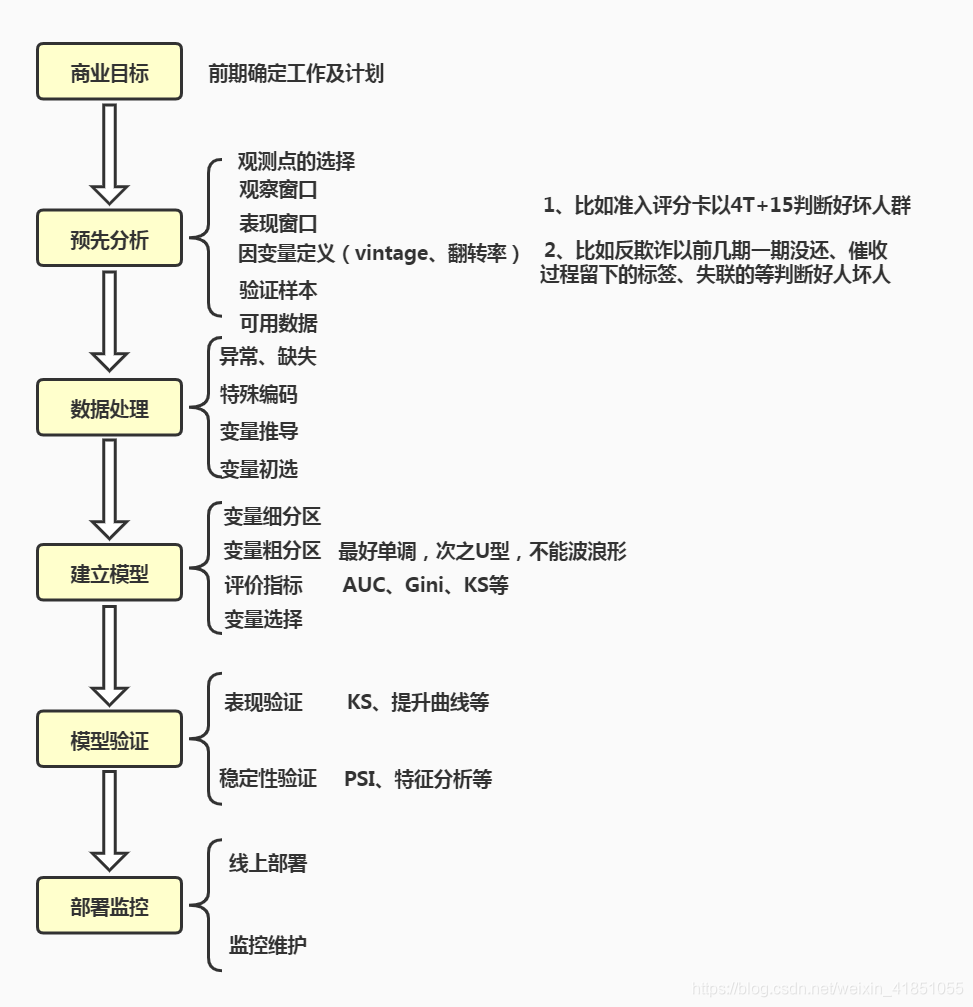
  log(odds)和评分之间具有线性关系

• 
  $PSI=sum_{i=1}^nln(frac{建模样本比例i}{验证样本比例i}*(建模样本比例i-验证样本比例i))$

  PSI=∑i=1n​ln(验证样本比例i建模样本比例i​∗(建模样本比例i−验证样本比例i))当PSI<0.2样本稳定

3.逻辑回归对数据的要求（比较严格）

输入数据必须是数值型数据、缺失值必须要填充、数据需要归一化或者标准化

4.逻辑回归的优缺点

优点：

• 形式简单、速度快、占用内存小（只需要各维度的特征值）
• 模型的可解释性好（假设性检验或者直接看各个特征对模型结果的影响）
• 模型效果不错（特征工程做的好）
• 方便输出结果阈值（阈值设定）

缺点：

• 容易欠拟合，相比较集成模型准确率不高
• 对数据要求较高（缺失、数据类型、异常、共线比较敏感）
• 处理非线性比较麻烦（非线性映射）
• 很难处理不平衡数据（高维、大量多类特征难以处理）
• 本身无法筛选特征

5.算法需要注意的点

为什么用极大似然估计作为损失函数

$theta_j:=theta_j-alphafrac{1}{m}sum_{i=1}^m(h_theta(x_i)-y_i)x_i^j$

θj​:=θj​−αm1​∑i=1m​(hθ​(xi​)−yi​)xij​更新速度只与
$x_i^j和y_i$

xij​和yi​相关，与sigmoid梯度无关，如果用平方损失函数会推导出更新的速度和sigmoid函数本身很相关。sigmoid在它定义域内梯度都不大于0.25，这样训练会非常缓慢。

训练过程中，有很多特征高的相关，会造成怎样的影响
损失函数最终收敛的情况下，最后不会影响分类效果。但是对于可解释性会产生很大的影响。（一方面权重分给了不同的特征，另一方面可能正负相互抵消）

为什么在训练过程中将高度相关的特征去掉
1、让模型的可解释性更好。2、大大提高训练速度。

为什么我们选自然对数作为成本函数（符合上面性质函数很多）
因为预测函数有sigmoid，函数中含有
$e^n$

en，其逆运算刚好是自然对数，最终会推导出形式优美模型参数的迭代函数，而不涉及指数或对数运算。

注：

• 理论与实践会有所差别，例如在处理样本不均衡时，评分卡并不是1:1效果最好，需要根据每个场景来实践
• 虽然模型比较偏技术，但是在整个流程当中需要业务的贯穿。无论从单变量的选择（可解释性）还是y标签的制定（vintage）等都需要强有力的业务解释