引言

 数模课上讲的微分方程部分的知识，在之前一直是笔者弱项，在此将基础知识稍作整理后汇总成此博文，不足之处，望笔者多多指正。

微分方程求解

Matlab求解析解

 在Matlab中解析解常用函数库dslove来进行求解，常用的语法格式：

dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’)
说明：在表达微分方程时，用字母D表示求微分，D2、D3等
表示求高阶微分.任何D后所跟的字母为因变量，自变量可以指
定或由系统规则选定为缺省

• 例子1：求取
  $frac{d u}{d t}=1+u^{2}$

  dtdu​=1+u2的通解。

dsolve('Du=1+u^2','t') 

• 例子2：求取
  $left{begin{array}{l} frac{d^{2} y}{d x^{2}}+4 frac{d y}{d x}+29 y=0 \ y(0)=0, y^{prime}(0)=15 end{array}right.$

  {dx2d2y​+4dxdy​+29y=0y(0)=0,y′(0)=15​ 的通解

y=dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x') 

• 例子3：求方程
  $left{begin{array}{l} frac{d x}{d t}=2 x-3 y+3 z \ frac{d y}{d t}=4 x-5 y+3 z \ frac{d z}{d t}=4 x-4 y+2 z end{array}right.$

  ⎩⎨⎧​dtdx​=2x−3y+3zdtdy​=4x−5y+3zdtdz​=4x−4y+2z​通解

x,y,z]=dsolve('Dx=2*x-3*y+3*z',... 　　'Dy=4*x-5*y+3*z','Dz=4*x-4*y+2*z', 't') 

Matlab求取数值解

 在生产和科研中所处理的微分方程往往很复杂,且大多得不出一般解．而实际中的对初值问题，一般是要求得到解在若干个点上满足规定精确度的近似值，或者得到一个满足精确度要求的便于计算的表达式。

求解原理

• 欧拉法
   在求解数值解过程中假设
  $x_{i+1}-x_{i}=h, quad i=0,1,2, cdots, n-1$

  xi+1​−xi​=h,i=0,1,2,⋯,n−1,那么可以尝试用离散的方式去接微分方程：
  $left{begin{array}{l} y^{prime}=f(x, y) \ yleft(x_{0}right)=y_{0} end{array}right.$

  {y′=f(x,y)y(x0​)=y0​​
  如果h步长较小，有：
  $y^{prime}(x) approx frac{y(x+h)-y(x)}{h}$

  y′(x)≈hy(x+h)−y(x)​
  可以得等到对应的欧拉公式：
  $left{begin{array}{l} y_{i+1}=y_{i}+h fleft(x_{i}, y_{i}right) \ y_{0}=yleft(x_{0}right) end{array} quad i=0,1,2, cdots, n-1right.$

  {yi+1​=yi​+hf(xi​,yi​)y0​=y(x0​)​i=0,1,2,⋯,n−1

• 使用数值积分(改进欧拉)

对方程f(x,y)两边由
$x_i$

xi​到
$x_{i+1}$

xi+1​进行积分，并利用梯形公式有：
$begin{aligned} yleft(x_{i+1}right)-yleft(x_{i}right) &=int_{x_{i}}^{x_{i+1}} f(t, y(t)) d t & approx frac{x_{i+1}-x_{i}}{2}left[fleft(x_{i}, yleft(x_{i}right)right)+fleft(x_{i+1}, yleft(x_{i+1}right)right)right] end{aligned}$

y(xi+1​)−y(xi​)​=∫xi​xi+1​​f(t,y(t))dt​≈2xi+1​−xi​​[f(xi​,y(xi​))+f(xi+1​,y(xi+1​))]​
得到：
$left{begin{array}{l} y_{i+1}=y_{i}+frac{h}{2}left[fleft(x_{i}, y_{i}right)+fleft(x_{i+1}, y_{i+1}right)right] \ y_{0}=yleft(x_{0}right) end{array}right.$

{yi+1​=yi​+2h​[f(xi​,yi​)+f(xi+1​,yi+1​)]y0​=y(x0​)​
结合欧拉公式使用可以得到：

$left{begin{array}{l} y_{i+1}^{(0)}=y_{i}+h fleft(x_{i}, y_{i}right) \ y_{i+1}^{(k+1)}=y_{i}+frac{h}{2}left[fleft(x_{i}, y_{i}right)+fleft(x_{i+1}, y_{i+1}^{(k)}right)right] k=0,1,2 end{array}right.$

{yi+1(0)​=yi​+hf(xi​,yi​)yi+1(k+1)​=yi​+2h​[f(xi​,yi​)+f(xi+1​,yi+1(k)​)]k=0,1,2​
满足精度条件后继续下一步的计算。

• 此外还可以结合泰勒公式继续得到比如龙格—库塔法、线性多步法等。

matlab求解

 语法格式：

[t，x]=solver(’f’,ts,x0,options)
(偷懒直接截图)

• 例子4：
  $left{begin{array}{c} frac{mathrm{d}^{2} x}{mathrm{d} t^{2}}-1000left(1-x^{2}right) frac{mathrm{d} x}{mathrm{d} t}-x=0 \ x(0)=2 ; x^{prime}(0)=0 end{array}right.$

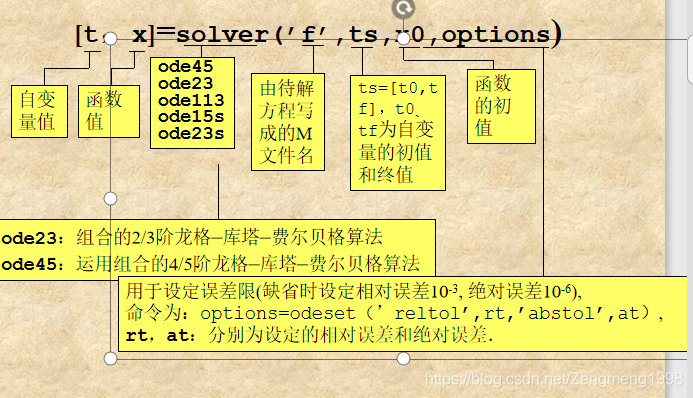
  {dt2d2x​−1000(1−x2)dtdx​−x=0x(0)=2;x′(0)=0​
  求解程序：

%例子4函数 function dy=vdp1000(t,y)     dy=zeros(2,1); dy(1)=y(2); dy(2)=1000*(1-y(1)^2)*y(2)-y(1); end  命令窗口： %例子4 t0=0; tf=3000; [T,Y]=ode15s('vdp1000',[0 3000],[2 0]); plot(T,Y(:,1),'-') 

运行结果：

• 例子5：
  $left{begin{array}{c} y_{1}^{prime}=y_{2} y_{3} \ y_{2}^{prime}=-y_{1} y_{3} \ y_{3}^{prime}=-0.51 y_{1} y_{2} \ y_{1}(0)=0, y_{2}(0)=1, y_{3}(0)=1 end{array}right.$

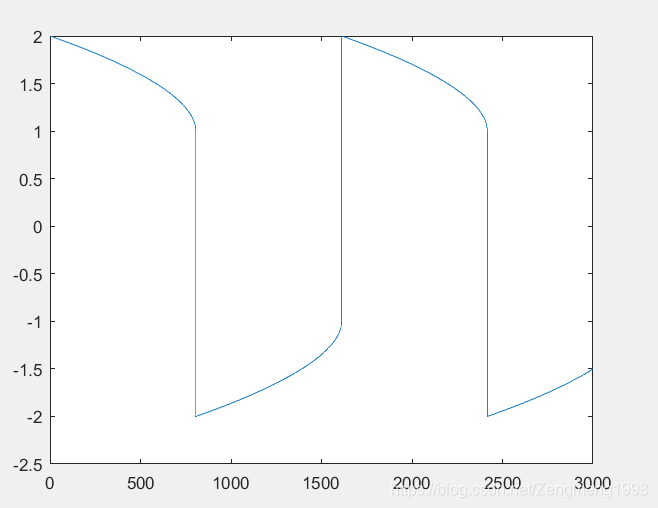
  ⎩⎪⎪⎨⎪⎪⎧​y1′​=y2​y3​y2′​=−y1​y3​y3′​=−0.51y1​y2​y1​(0)=0,y2​(0)=1,y3​(0)=1​
  求解程序：

%求解例子5 function dy=rigid(t,y)        dy=zeros(3,1); dy(1)=y(2)*y(3); dy(2)=-y(1)*y(3); dy(3)=-0.51*y(1)*y(2); end  命令行： t0=0;  tf=12;  [T,Y]=ode45('rigid',[0 12],[0 1 1]); plot(T,Y(:,1),'-',T,Y(:,2),'*',T,Y(:,3),'+') 

结果：

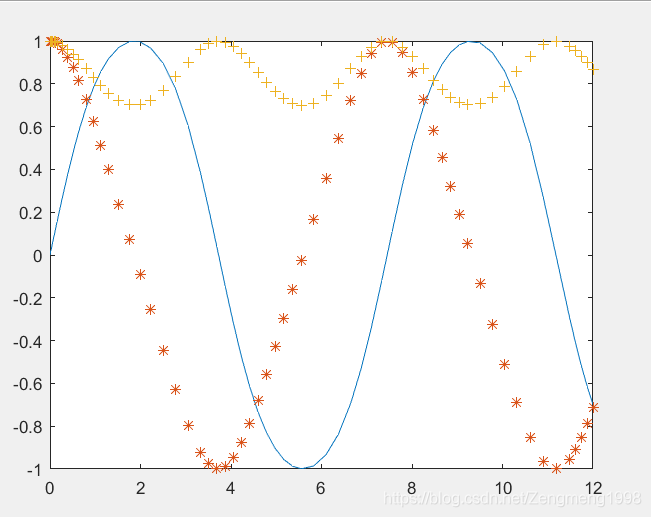
小结

 在笔者本科阶段的学习过程中，微分求解方程的学习经历课程主要有：常微分方程、数值分析、数学建模。希望在未来的学习过程中将其进一步的串成网络。最后本文不足之处望多多指正。

一段

某程序员夫妇新婚，一年之后喜得贵子，取名”灵灵”
过一年后又喜得一女，取名”灵伊”
两年之后得子”伊灵”
两年之后，夫妇商定为得圆满再生一子，取名”伊伊”
不料产科发现所怀为双胞胎，夫欲减胎，妻不允，冥思许久，对夫曰:“老五就叫’忆初’吧…”