本文代码对应的github地址:https://github.com/nieandsun/redis-study 前段时间项目里加上了布隆过滤器,本文简单从guava源码的角度做一些分析 —》 其实主要是为自己答疑解惑!!! 我觉得布隆过滤器在互联网环境的使用场景用下面这幅图就可以描述的很清楚,这里我就不过多去叙述了。 这里直接引用文章https://www.jianshu.com/p/bef2ec1c361f对布隆过滤器原理的叙述: BF是由 当要 当要 下图示出一个m=18, k=3的BF示例。集合中的x、y、z三个元素通过3个不同的哈希函数散列到位数组中。当查询元素w时,因为有一个比特为0,因此w不在该集合中。 说实话其实布隆过滤器的原理,我在上学的时候就知道了,但是刚看这个原理的时候,不知道你有没有过这样的困惑 + 思考过程: (1)首先应该明确的是,当你拿着一个值去布隆过滤器里去查询时,只要布隆过滤器拿着你这个值有一次hash运算发现对应位置的值为0, 则就可以明确的说明,该值不存在 —> (2)问题在于,假设数组里有很多位置都变为1了,那错判率(又叫容错率)岂不会很大 —> 因此,可以想像为了降低 容错率,肯定是数组越长越好 —> 但是肯定又不能无限长,因为那样占用的存储空间就会很大!!! (3)还有就是hash函数的个数,如果只有一个hash函数,那就很有可能由于hash碰撞而发生错判 —> 但是如果hash函数过多,那由0变为1的位置也会变多 —> 这样好像也会致使错判率升高!!! —> 因此hash函数的个数,到底怎样才算合理呢??? 这玩意,我觉得单靠自己去想,尤其是第(3)个问题,我觉得抓破头皮也不一定能想明白 —> 还好,Google的工程师替我们去想了,并将布隆过滤器的算法,集成到了guava包里!!! 首先guava包,想必大家应该都知道,其maven依赖如下: 布隆过滤器 比如说我们可以说HashMap也是一个算法 + 数据结构构成的容器,其底层用到了数组、链表、红黑树等数据结构,往map容器里put值用到了hash算法,为了降低hash碰撞又用到了高16位低16位进行与运算的算法等等 || 从map里取值又用到了数组遍历、链表遍历、红黑树遍历对应的算法等等 与之类似, 布隆过滤器也是一个算法 + 数据结构构成的容器,其底层的数据结构就是一个bit数组,往布隆过滤器里放值的过程,其实就是拿着该值经过指定次数的hash运算 ,并将运算结果对应位置的值由0改为1( 初始化一个布隆过滤器的方法有如下几个: 也就是说初始化一个布隆过滤器,必须要指定的两个参数是 特别简单,即调用布隆过滤器的put方法 也特别简单,就是调用布隆过滤器的contains方法 简单看一眼运行结果: 再回过头去看我在本文第3小节的疑惑 与 思考,其实我们不难发现,要想真正把布隆过滤器的思想进行落地,最最重要的肯定就是要解决两个问题: 我们拿着 (1)首先在调用create进行初始化布隆过滤器时,可以看到默认情况下布隆过滤器的容错率为0.03 —》 这就解释了为什么我们4.2.4中的错判率约为0.03的原因。 (2)继续跟断点,可以在BloomFilter源码的350、351两行看到我们想要的答案 我贴这两段代码想说明啥呢? (3)接着我们来看一下它计算出的结果: 对4.2.4中的代码稍作修改,我们假设我们的数据量有1千万,规定的容错率为:0.00001,则才需要用到的内存大小为239626459位,经过换算后如下: 这里看一下阿里的《Java开发手册》,可知数据库单表行数据超过500行,就可以考虑分库分表了: (2) 我们只需要28.6M的内存就可以保证:同一时间10万个恶意请求,只有一个左右的请求可以真正到达我们的数据库。。。 (3)说到这里,其实还有一个问题:或许有些互联网公司,会搭建比较庞大的redis集群,此时redis内某类数据的数据量可能会远远大于1千万,此时要万一有人就是要攻击你的redis集群,那第1小节中第二个图的架构模式,就非常有必要了,有兴趣的可以clone下来代码,自己测算一下。 由此可知,布隆过滤器在解决缓存击穿问题上确实非常有效!!! 最后提醒一下,请格外注意一下,第5小节,注释掉的那段话
文章目录
1 布隆过滤器在互联网环境的使用场景简介
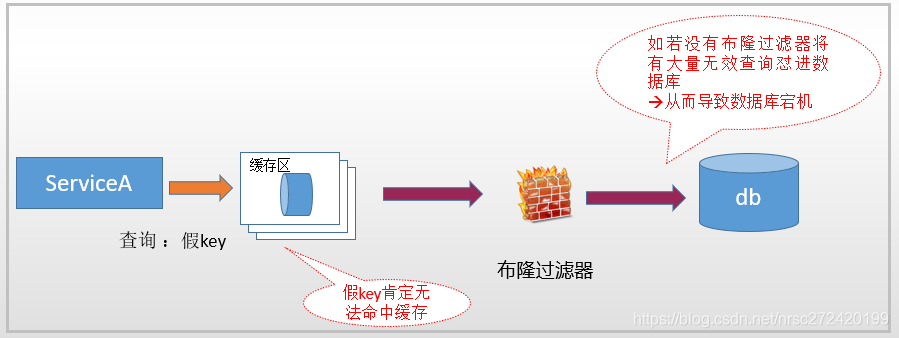
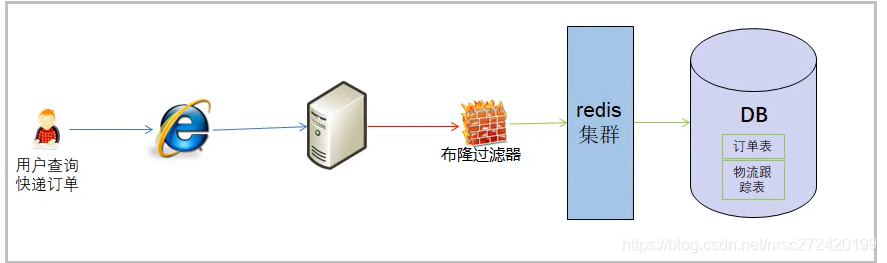
当然有些项目,或许也会这样使用布隆过滤器:
2 布隆过滤器的原理
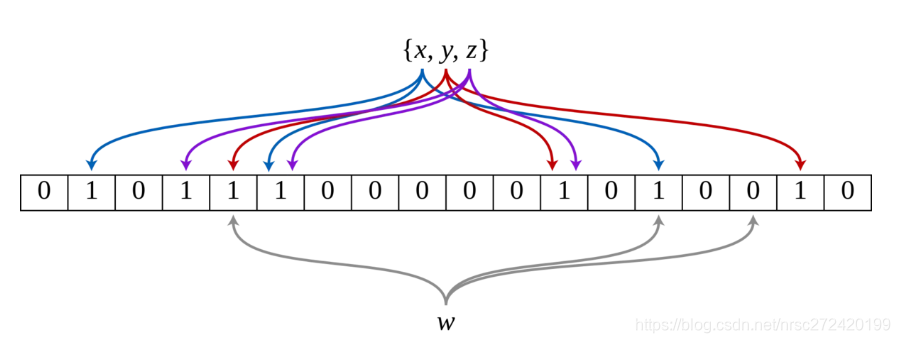
一个长度为m比特的位数组(bit array)与k个哈希函数(hash function)组成的数据结构。位数组均初始化为0,所有哈希函数都可以分别把输入数据尽量均匀地散列。
插入一个元素时,将其数据分别输入k个哈希函数,产生k个哈希值。以哈希值作为位数组中的下标,将所有k个对应的比特置为1。
查询(即判断是否存在)一个元素时,同样将其数据输入哈希函数,然后检查对应的k个比特。如果有任意一个比特为0,表明该元素一定不在集合中。如果所有比特均为1,表明该集合有(较大的)可能性在集合中。为什么不是一定在集合中呢?因为一个比特被置为1有可能会受到其他元素的影响,这就是所谓“假阳性”(false positive)。相对地,“假阴性”(false negative)在BF中是绝不会出现的。

3 我对 布隆过滤器 困惑 + 思考
这点是毋庸置疑的!!!
4 布隆过滤器在guava中具体是个啥
<dependency> <groupId>com.google.guava</groupId> <artifactId>guava</artifactId> <version>19.0</version> </dependency>
4.1 通过与HashMap对比,简单理解一下guava中的布隆过滤器到底是什么
按照我的理解,它其实就是一个算法 + 数据结构的结合体,其本质其实是一个容器。我觉得其实可以将其与HashMap进行类比:
不存储该值,这里一定要注意) || 验证某个值是否在布隆过滤器里时,就拿着该值再次经过指定次数的hash运算,并看看运算结果对应的位置是否有为0的,只要有一个hash运算结果对应的位置为0,就表明该值没有往布隆过滤器里放过。
4.2 guava中布隆过滤器API简介
4.2.1 初始化一个布隆过滤器的方式 — 类似于new一个HashMap
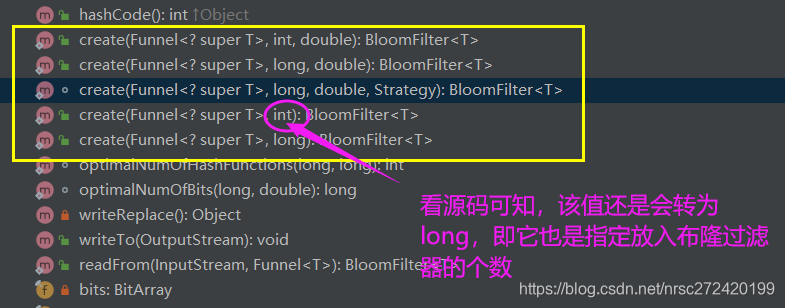
以上面第3个create方法为例进行一下简单介绍:
4.2.2 往布隆过滤器里放值的方式
4.2.3 判断某个值是否在布隆过滤器里
4.2.4 通过一个简单的栗子,看一下布隆过滤器的API使用姿势
public class BloomFilterTest { private static final int insertions = 1000000; @Test public void bfTest() { //初始化一个存储String数据的布隆过滤器,初始化大小100W BloomFilter<String> bf = BloomFilter.create(Funnels.stringFunnel(Charsets.UTF_8), insertions); //初始化一个存储String数据的set,初始化大小100w //Set<String> sets = new HashSet<>(insertions); Set<String> sets = Sets.newHashSetWithExpectedSize(insertions); //用guava进行new HashSet() 的方式,与上面的代码一个意思 //初始化一个存储String数据的set,初始化大小100w //List<String> lists = new ArrayList<String>(insertions); ArrayList<String> lists = Lists.newArrayListWithCapacity(insertions);//用guava进行new HashSet() 的方式,与上面的代码一个意思 //向三个容器初始化100万个随机并且唯一的字符串 , 100万个uuid 34M多 for (int i = 0; i < insertions; i++) { String uuid = UUID.randomUUID().toString(); bf.put(uuid); sets.add(uuid); lists.add(uuid); } int wrong = 0;//布隆过滤器错误判断的次数 int right = 0;//布隆过滤器正确判断的次数 /**** * 相信你耷眼一看就知道,这10000次循环里,会有100个肯定是在布隆过滤器里存在的 * 剩下10000 - 100个肯定是不在布隆过滤器里的 */ for (int i = 0; i < 10000; i++) { String test = i % 100 == 0 ? lists.get(i / 100) : UUID.randomUUID().toString();//按照一定比例选择bf中肯定存在的值 if (bf.mightContain(test)) { if (sets.contains(test)) { right++; } else { wrong++; } } } System.out.println("=============right=============" + right); System.out.println("=============误判率=============" + wrong / 10000.0); } }
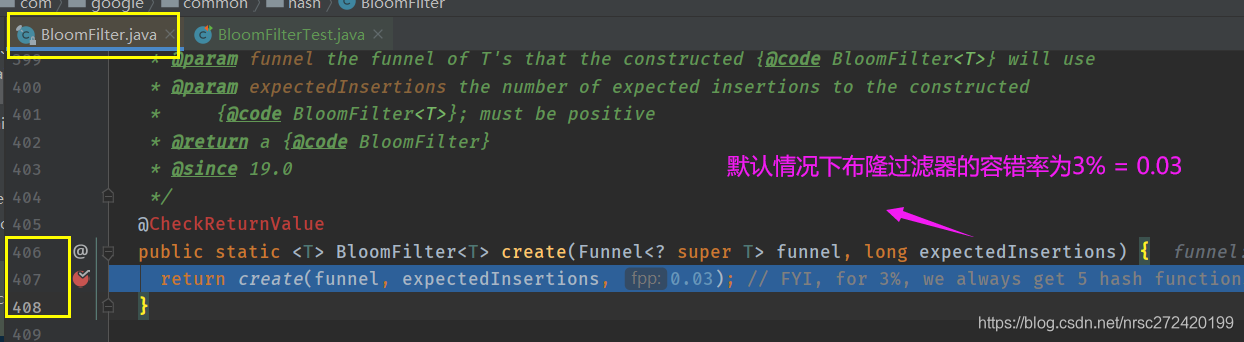
5 简单从guava源码的角度为自己解解惑
4.2.4 中的代码打着断点看一下:
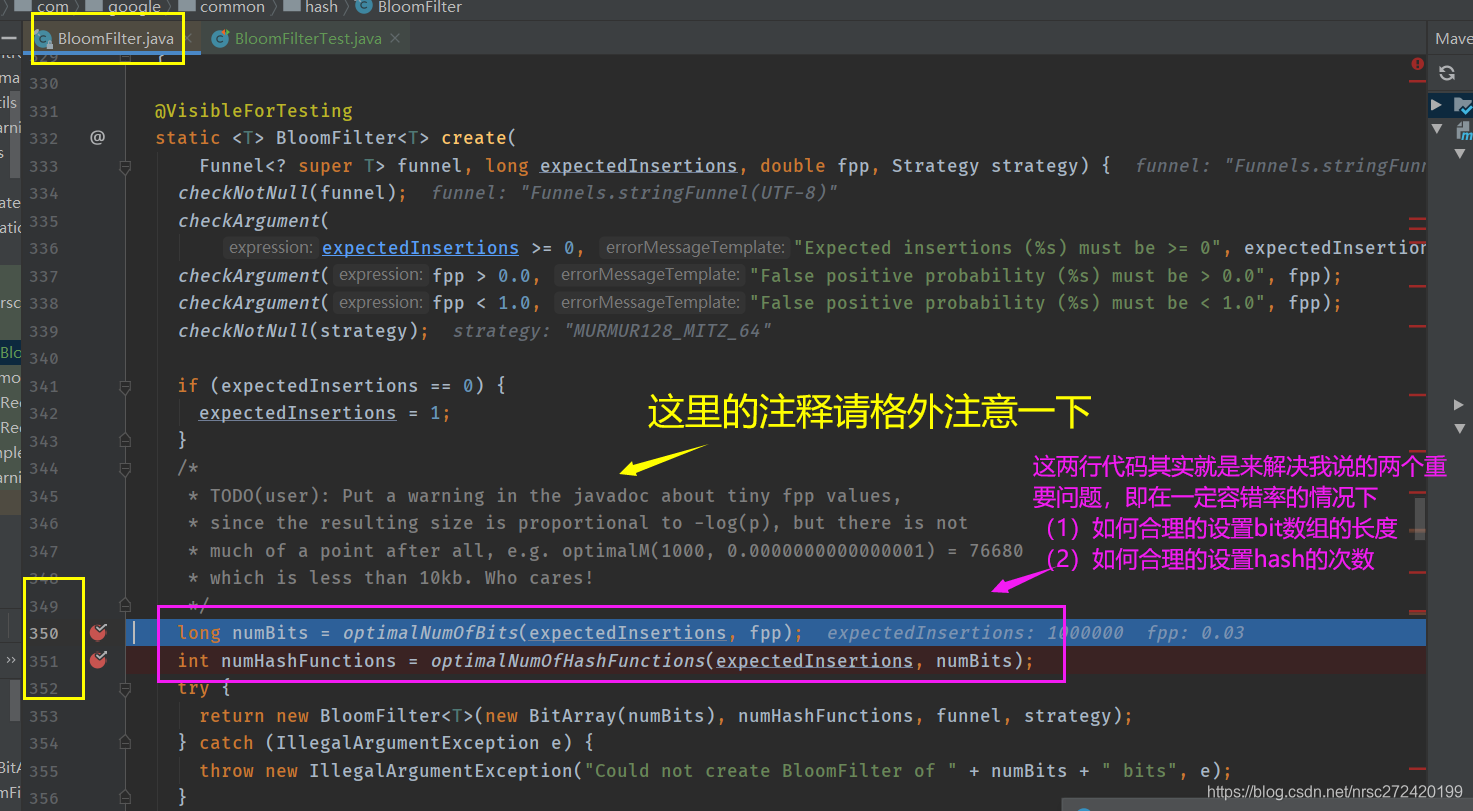
这里贴一下计算bit合理长度以及hash合理次数的源码: /** * Computes m (total bits of Bloom filter) which is expected to achieve, for the specified * expected insertions, the required false positive probability. * * See https://en.wikipedia.org/wiki/Bloom_filter#Probability_of_false_positives for the formula. * * @param n expected insertions (must be positive) * @param p false positive rate (must be 0 < p < 1) */ @VisibleForTesting static long optimalNumOfBits(long n, double p) { if (p == 0) { p = Double.MIN_VALUE; } return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2))); } /** * Computes the optimal k (number of hashes per element inserted in Bloom filter), given the * expected insertions and total number of bits in the Bloom filter. * * See https://en.wikipedia.org/wiki/File:Bloom_filter_fp_probability.svg for the formula. * * @param n expected insertions (must be positive) * @param m total number of bits in Bloom filter (must be positive) */ @VisibleForTesting static int optimalNumOfHashFunctions(long n, long m) { // (m / n) * log(2), but avoid truncation due to division! return Math.max(1, (int) Math.round((double) m / n * Math.log(2))); }
numBits = 7298440
numHashFunctions = 5
这表明 : 在布隆过滤器里放置1千万个数据,我们随机拿n个数据,判断这n个数据是否在布隆过滤器里存过,在错判率为0.03时,需要7298440位的内存大小,经过换算后可以发现,不到1M。

6 互联网场景使用布隆过滤器的可行性分析
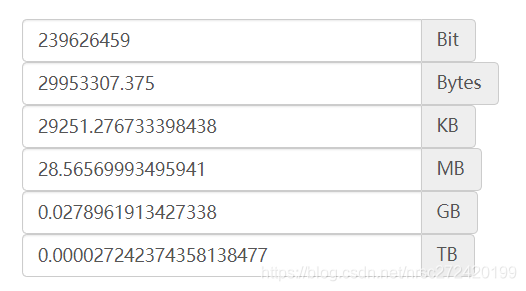
这是什么概念呢?
(1)假设我们的数据库里有1千万个值 —> 这其实应该是一个比较大的数字了

end!!!
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)