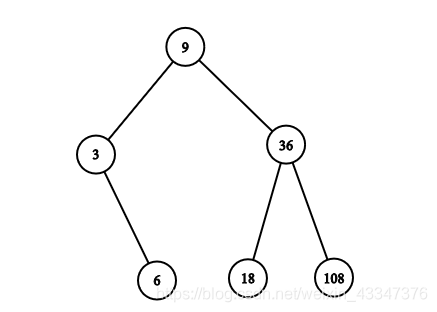
在瑞神大战宇宙射线中我们了解到了宇宙狗的厉害之处,虽然宇宙狗凶神恶煞,但是宇宙狗有一个很可爱的女朋友。 最近,他的女朋友得到了一些数,同时,她还很喜欢树,所以她打算把得到的数拼成一颗树。 这一天,她快拼完了,同时她和好友相约假期出去玩。贪吃的宇宙狗不小心把树的树枝都吃掉了。所以恐惧包围了宇宙狗,他现在要恢复整棵树,但是它只知道这棵树是一颗二叉搜索树,同时任意树边相连的两个节点的gcd(greatest common divisor)都超过1。 但是宇宙狗只会发射宇宙射线,他来请求你的帮助,问你能否帮他解决这个问题。 GCD:最大公约数,两个或多个整数共有约数中最大的一个 ,例如8和6的最大公约数是2。 一个简短的用辗转相除法求gcd的例子: 输入第一行一个t,表示数据组数。 对于每组数据,第一行输入一个n,表示数的个数 接下来一行有n个数,输入保证是升序的。 每组数据输出一行,如果能够造出来满足题目描述的树,输出Yes,否则输出No。 无行末空格。 第一个样例可以构建下图所示的二叉搜索树 这道题开始没想到用区间dp来做,想了一个自己认为“绝妙的方法”。利用栈来维护一条主链,方法就不说了,毕竟结果炸了。这个方法挺“绝命的”,样例全过,直接0分。 二叉搜索树具有明显的子结构特性,这个题虽然要构成一个二叉树,但是给出的是一个区间,因此这个题还是要用区间dp来做的,树的结构不能丢,我们定义两个数组: 然后用 当 状态转移是每次转移一个点,在
问题描述
补充知识:
int gcd(int a,int b){return b == 0 ? a : gcd(b,a%b);} Input
Output
Sample input & output
Sample input1
1 6 3 6 9 18 36 108 Sample output1
Yes Sample input2
2 2 7 17 9 4 8 10 12 15 18 33 44 81 Sample output2
No Yes 数据范围
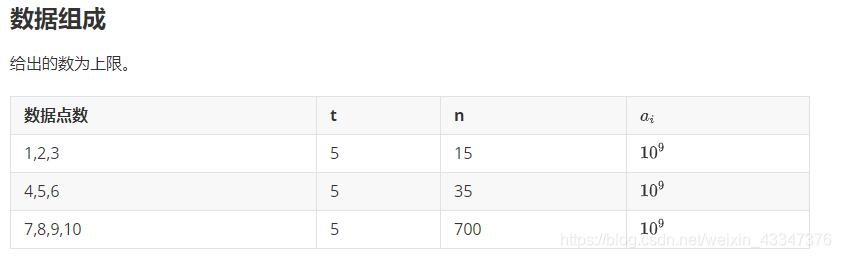
提示
解题思路
l[i][j],r[i][j]分别表示以
i为根,向左到
j可以作为
i的左子树,向右到
j可以作为
i的右子树。树结构非常重要,虽然是区间dp,但是这个结果要构成一个二叉搜索树,因此必须有这两个数组。
dp[i][j]表示
i∼j能构成一棵树。函数最后返回
dp[1][n]。(我以前尝试过直接
dp[i][j]表示
i∼j能构成一棵树,然后拼接用
dp[i][k],dp[k][j]拼接,这样错的原因是,
dp[i][k]能够构成一棵树,不一定表示左子树,
dp[k][j]能够构成一棵树,不一定表示右子树,那么就不一定能拼接起来。2,3,5,30这样四个节点数据就可以卡死。)
l[k][i]==r[k][j]==true时,
dp[i][j]=true,此时
i∼j是以
k为根的二叉搜索树。
dp[i][j]=true的情况下:
l[j+1][i]∣=gcd(a[j+1],a[k]),(i≤k≤j)r[i−1][j]∣=gcd(a[i−1],a[k]),(i≤k≤j)
转移方程为什么这么写呢,先看第一个方程,首先这个时候我们已经保证了从
i到
j这段区间可以构成一棵二叉搜索树,并且根节点是
k,注意这个根节点很重要。如果说
gcd(a[j+1],a[k])>1了,那么二者之间就可以连边,并且注意
l数组的定义:表示以
i为根,向左到
j可以作为
i的左子树,那么
a[j+1]的左儿子就是
a[k]了。在枚举
k的过程中,只要有一次可以连边,那么
l[j+1][i]=true。所以中间使用的是
∣=符号。第二个方程同理。完整代码
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <cstring> #include <string> #include <algorithm> using namespace std; const int maxn=700+100; int t,n,a[maxn]; bool dp[maxn][maxn],g[maxn][maxn],l[maxn][maxn],r[maxn][maxn]; int gcd(int _a,int _b) {return _b==0? _a: gcd(_b,_a%_b);} void init(){ memset(l,false,sizeof(l)); memset(r,false,sizeof(r)); memset(dp,false,sizeof(dp)); for (int i=1; i<=n; i++) { l[i][i]=r[i][i]=dp[i][i]=true; for (int j=1; j<=n; j++) g[i][j]=gcd(a[i],a[j])>1; } } bool IsBinarySearchTree(){ for (int len=1; len<=n; len++){ for (int i=1; i<=n-len+1; i++){ int j=i+len-1; for (int k=i; k<=j; k++){ if(l[k][i] && r[k][j]){ dp[i][j]=true; l[j+1][i]|=g[j+1][k]; r[i-1][j]|=g[i-1][k]; } } } } return dp[1][n]; } int main(){ scanf("%d",&t); while(t--){ scanf("%d",&n); for (int i=1; i<=n; i++) scanf("%d",&a[i]); init(); if(IsBinarySearchTree()) printf("Yesn"); else printf("Non"); } return 0; }
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)