图的基本概念及图演算法壮壮不太胖的学习笔记-

回顾：数据的逻辑结构

一，图的定义的基本术语

图： G =（V，E）

• V：顶点(数据元素)的有穷非空集合；
• E：边的有穷集合。

无向图(Undirected graph)： 每条边的没有方向，eg：G1

• 無向圖G=(V,E)，V代表點集合，E代表邊集合。E 中的元素形式為集合 {u,v}，代表邊的兩端。

有向图(Directed graph)： 每条边都有方向，eg：G2

• 有向圖G=(V,E)，V代表點集合，E代表邊集合。E 中的元素形式為 (u,v)，u代表起點，v代表中點。
  

完全图： 任意两个顶点都有一条边相连（有去有回）

稀疏图： 有很少边或弧的图（e < n*log n）。

稠密图： 有较多边或弧的图。

网： 边 / 弧带权值的图。

邻接： 有边 / 弧相连的两个顶点之间的关系。

• 存在（v_i，v_j），则称 v_i 和 v_j 互为邻接点；
• 存在 <v_i，v_j>，则称 v_i 邻接到 v_j，v_j 邻接于 v_i。

关联(依附)： 边 / 弧与顶点之间的关系。

顶点的度： 与该顶点相关联的边的数目，记为：TD(v)

• 在有向图中，顶点的度等于该点的入度与出度之和。
• 顶点v的入度是以v为终点的有向边的条数，记作：ID(v)
• 顶点v的出度是以v为始点的有向边的条数，记作：OD(v)
  

那么，问：当有向图中仅1个顶点的入度为0，其余顶点的入度均为1，此时是什么形状？（答案：有向树，如下图）

路径： 接续的边构成的顶点序列。
路径长度： 路径上边或弧的数目 / 权值之和。
例，有无向图如上图，由 v₅ 到 v₃ 的路径可以是 [v₅，v₂，v₃] 也可以是 [v₅，v₄，v₃] 或 [v₅，v₂，v₄，v₃] 和 [v₅，v₄，v₂，v₃]。它们的路径长度分别为 2，2，3，3；若有权值的话需要将权值相加。

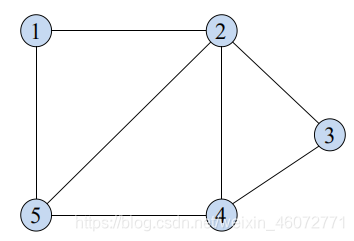
回路(环)： 第一个顶点和最后一个顶点相同的路径。（起点与重点相同）
简单路径： 除路径起点和终点可以相同外，其余顶点均不相同的路径。
简单回路(简单环)： 除路径起点和终点相同外，其余顶点均不相同的路径。

（a）简单路径：0 – 1 – 3 – 2，起点终点可以不同，但不能出现重复顶点。
（b）非简单路径：0 – 1 – 3 – 0 – 1 – 2，顶点 v₀ 和 v₁ 重复了。
（c）回路：0 – 1 – 3 – 0，起点和终点均为 v₀

连通图(强连通图)： 在无(有)向图 G = ( V, {E} )中，对任意两个顶点v、u，都存在从 v 到 u 的路径，则称G是连通图(强连通图)。

权与网： 图中边或弧所具有的相关数称为权（表明从一个顶点到另一个顶点的距离或耗费）。带权的图称为网。

子图： 设有两个图 G = ( V, {E} ) 和 G1 = ( V1, {E1} )，若 V1 包含于 V，E1 包含于 E，则称 G1 是 G 的子图。

连通分量(强连通分量)

• 将非连通图分为了若干连通的部分；
• 无向图G的极大连通子图称为 G的连通分量
  极大连通子图意思是：该子图是 G 连通子图，将 G 的任何不在该子图中的顶点加入，子图不再连通。
  
• 有向图G的极大强连通子图称为 G的强连通分量
  极大强连通子图意思是：该子图是 G 的强连通子图，将 G 的任何不在该子图中的顶点加入，子图不再是强连通的。
  
  极小连通子图： 该子图是G 的连通子图，在该子图中删除任何一条边子图都不再连通。
  生成树： 包含无向图G 所有顶点的极小连通子图。
  生成森林： 对非连通图，有各个连通分量的生成树的集合
  

二，邻接（Adjacency）

首先回顾一下上边提到的邻接，什么是邻接
邻接： 有边 / 弧相连的两个顶点之间的关系。

• 存在（v_i，v_j），则称 v_i 和 v_j 互为邻接点；
• 存在 <v_i，v_j>，则称 v_i 邻接到 v_j，v_j 邻接于 v_i。

2.1 列表表示（Adjacency-List）

无向图
可藉由 Adjacency-list 表示，将每一个相邻的点集合用一个List 存起來。

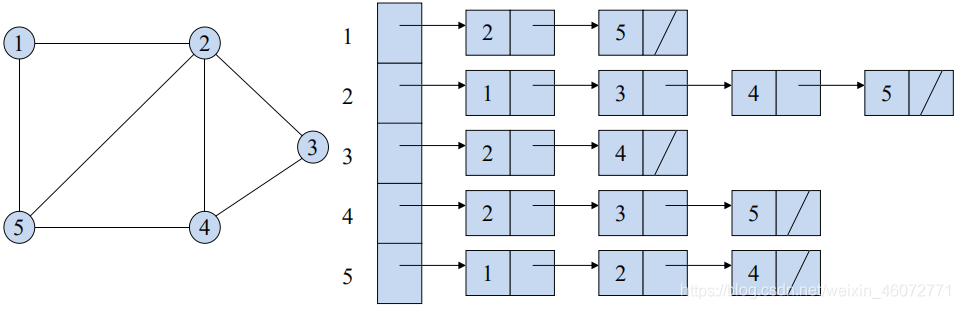
有向图
可藉由Adjacency-List表示，將每個點所指向的點集合存在List中。

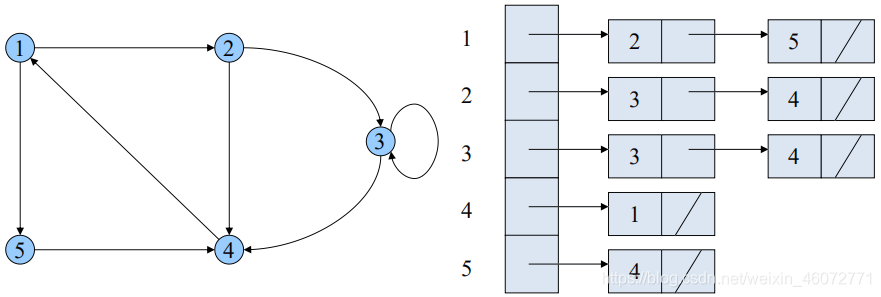
2.2 矩阵表示（Adjacency-Matrix）

无向图
可藉由 Adjacency-Matrix 表示，利用一個二維矩阵將每對點之間是否有邊連起來；

• 有存1；
• 沒有存0。
  
  有向图
  可藉由 Adjacency Matrix 表示，利用一個二維矩阵A
• 若(u,v)是一個邊則A[u][v]=1 ，由 u 指向 v
• 反之 A[u][v]=0。
  

三，图的遍历

遍历定义：

• 从已给的连通图中的某一顶点出发，沿着一些边访遍图中所有的顶点，且使每一个顶点仅被访问一次，就叫做图的遍历，他是图的基本运算。
  

遍历实质： 找每个顶点的邻接点的过程。

图的特点： 图中可能存在回路，且图的任一顶点都可能与其他顶点相同，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问的顶点。（例如，图中v₂ 和 v₃）

那么如何避免重复访问？
解决思路：设置辅助数组 visited[ n ]，用来标记是否访问过该顶点

• 初始状态为 visited[ i ] = 0
• 顶点 v_i 被访问时，改 visited[ i ] = 1，以此来避免多次访问。

图的常用遍历

• 深度优先搜索（Depth_First Search —- DFS）
• 广度优先搜索（Breadth_First Search —- BFS）

3.1 深度优先搜索（DFS）

参考：视频讲解 青岛大学–王卓
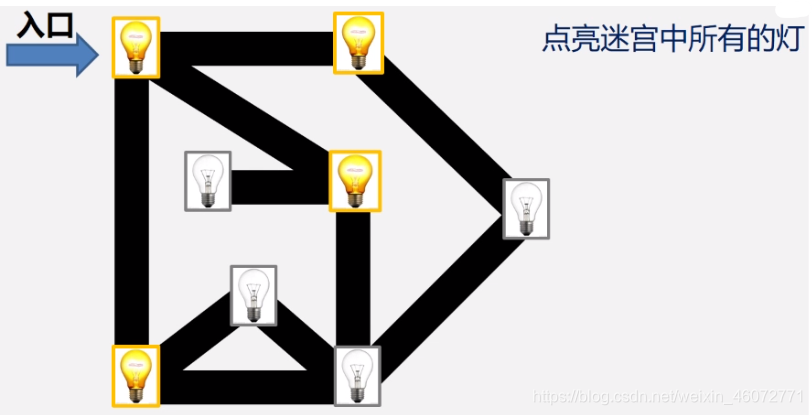
引例：点亮所有的灯
思路：选择一条路径，已知走到没有未点亮的灯或到尽头时再回头，每次退一步，若有未点亮的灯则选择该点，若没有未点亮的灯则再退回一步，直到所有灯全部都被点亮。

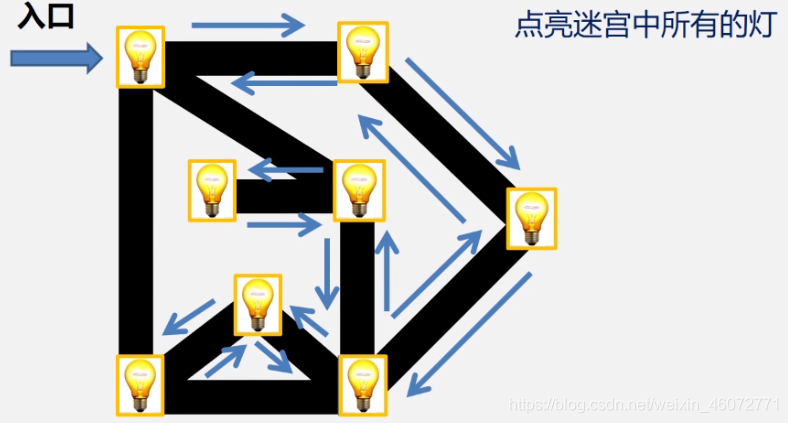
最初的选择不同，会有不同的访问路径。

3.1.1 深度优先搜索遍历算法的实现

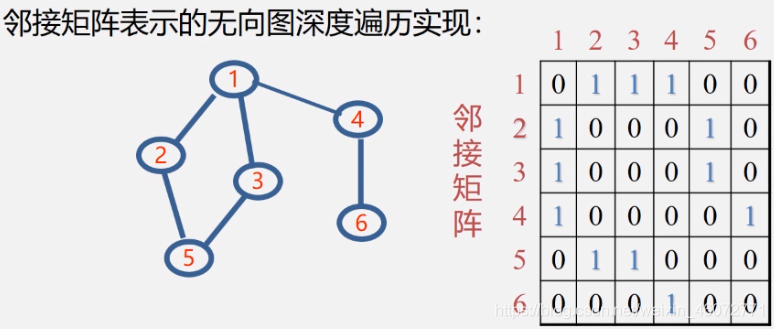
设置辅助数组 visited[ n ] = [ 0，0，0，0，0，0 ]，分别对应每一个顶点 v_i

首先，我们选择 v₂ 为起始点，则 visited[ 1 ] = 1（ visited[ n ] = [ 0，1，0，0，0，0 ] ）
然后来看邻接矩阵，只看 v₂ 这一行就可以，可以看出与 v₁ 相连，则我们走到顶点 v₁（设置 visited[ 0 ] = 1；visited[ n ] = [ 1，1，0，0，0，0 ]）；

接下来，看邻接矩阵 v₁ 这一行，可以看出 v₂、v₃、v₄ 均与 v₁ 相连，则从后两者之间做出选择，选择 v₃（设置 visited[ 2 ] = 1；visited[ n ] = [ 1，1，1，0，0，0 ]）；

以此类推，下一个邻接点为 v₅（设置 visited[ 4 ] = 1；visited[ n ] = [ 1，1，1，0，1，0 ]） ，接下来与 v₅ 邻接的 v₂、v₃ 均已经访问过，则依次退回 v₂、v₁，发现有未访问的点 v₄，则选该点为下一个邻接点，之后一直重复上述操作。。。

最终达到 visited[ n ] = [ 1，1，1，1，1，1 ]，访问路径为 v₂ – v₁ – v₃ – v₅ – v₄ – v₆

void DFS(AMGraph G, int v){ //图G为邻接矩阵类型  cout<<v; //访问第v个顶点  visited[v] = true; //依次检查邻接矩阵v所在的行 for(w = 0; w < G.vexnum; w++) if((G.arcs[v][w] != 0)&&(!visited[w])) DFS(G, w), //w是v的邻接点，如果w未访问，则递归调用DFS } 

3.1.2 DFS 算法效率分析

用邻接矩阵来表示图（假设有 n 个顶点，则为 n*n矩阵）

• 遍历图中每一个顶点都要从头扫描该顶点所在的行
• 时间复杂度为 O(n²)

用邻接表表示图

• 虽然有 2e 个表结点，但只需要扫描 e 个结点即可完成遍历，加上访问 n 个头结点的时间
• 时间复杂度为 O(n + e)

结论：

• 稠密图（边较多）适于在邻接矩阵上进行深度遍历；
• 稀疏图（边少 e < n*log n）适于在邻接表上进行深度遍历。

3.1.3 非连通图的遍历

以上图为例：
首先，以a为初始点（随机的），接下来按照上边的步骤依次找到邻接点直到全部都访问过（该连通分量已经遍历完成），因为我们知道是非连通图，则我们在没有访问过得顶点中再随机找一个顶点开始新的遍历。

3.2 广度优先搜索（BFS）

参考：视频讲解 青岛大学–王卓
与DFS不同，广度优先搜索是先选定一个初始点，然后访问他所有的邻接点，如下图所示

方法：

• 从图的某一节点出发，首先依次访问该节点的所有邻接点 v_i1、v_i2、…、v_in；
• 再按这些顶点被访问的先后次序访问与他们想邻接的所有未被访问的顶点；
• 重复此过程，直至所有顶点均被访问为止。

其实就是一层一层的访问，如下例

非连通图的广度遍历

3.2.1 实现和步骤

以上图为例：

1. 首先我们需要两个辅助数组
   visited[ n ] = [ 0，0，0，0，0，0，0，0 ] 用来记录顶点是否访问过，访问后设置 visited[ i ] = 1；
   next[ n ] = [ -1，-1，-1，-1，-1，-1，-1，-1 ] 用来记录访问点的所有未访问邻接点；
2. 选择 v₁ 为初始点，则记录 visited[ 0 ] = 1 和 next[ n ] = [ 1，2，3，-1，-1，-1，-1，-1 ]， v₁ 的邻接点是 v₂、v₃
3. 然后依次访问 v₂、v₃，并记录 visited[ 1, 2 ] = 1 并且 next[ n ] = [ 1，2，3，4，5，6，7，-1 ]；
4. 依照上边的步骤继续访问顶点4567并记录他们的邻接点
5. 最终使得
   visited[ n ] = [ 1，1，1，1，1，1，1，1 ]
   next[ n ] = [ 1，2，3，4，5，6，7，8 ]
6. 当 visited[ n ]中所有元素均为 1，next[ n ]中没有任何元素为 -1 时候说明迭代完成。

3.2.2 BFS 算法及其效率

void BFS(Graph G, int v){ // 按广度优先非递归遍历连通图G  cout<<v; // 访问第 v 个顶点  visited[v] = true; InitQueue(Q); // 辅助队列Q初始化，置空 EnQueue(Q, v); // v 进队 while(!QueueEmpty(Q)){ // 队列非空 DeQueue(Q, u); // 队头元素出队并置为 u for(w = FirstAdjVex(G,u);w >= 0;w = NextAdjVex(G, u, w)) if(!visited[w]){ // w 是 u尚未访问的邻接点    cout<<w;      visited[w] = true; EnQueue(Q, w); // w 进队 }// }// }// 

BFS 算法效率分析

• 如果使用邻接矩阵，则BFS对于每一个被访问到的顶点，都要循环检测矩阵中的整整一行（n 个元素），总的时间代价为 O( n² )。
• 用邻接表来表示图，虽然有 2e 个表结点，但只需要扫描 e 个结点即可完成遍历，加上访问 n 个头结点的时间，时间复杂度为 O( n + e )。

更多关于图的应用：

• 什么是最小生成树以及如何构建
• 使用Dijkstra/Floyd算法解决最短路径问题
• 什么是拓扑排序及其Python实现
• 10分钟了解关键路径及如何求得关键路径