前言 这是我听老师讲课做的笔记,考试要看的。 第一步接下来的课经常用 不管是链式存储或者顺序存储,都有一种基本的存储方式,叫做按值查找,要想查找一个数,都要一个个问。这里讲顺序查找就行了 (1)顺序查找又称线性查找,是最基本的查找方法之一。 (2)基本思想 :从表的一端开始逐个进行记录的关键字和给定值的比较。 存储结构: !算法实现 要求能写出来 性能分析:倒着比较 平均比较次数(设等概率Pi=1/n) 就上述算法而言,对于n个数据元素的表,给定值k与表中第i个元素关键码相等,即定位第i个记录时,需进行 查找成功时: ASLs = Pi*(n-i+1)=(1+2+3+….+n)/n = (n+1)/2 顺序查找的平均查找长度为: 缺点:查找效率低,n较大时不宜采用。 使用这种方法,对表有 两点要求: (1)表只能顺序存储 (2)表中的元素必须有序排列 (3)(2)已经排好顺序了,用折半查找(二分查找)来实现。 先确定待查记录所在范围,然后取中间元素作为比较对象,若相等,则查找成功,否则如果小于中间元素则将查找区域缩小到左半部分,否则缩小到右半部分,直到找到或找不到该记录为止。 mid low high指的是他的下标 (1) 确定区间的中间位置 (2) 用给定值与中间位置的关键字值比较: 若相等,则查找成功; 若给定值大,新查找区为后半区: 若给定值小,新查找区为前半区: 对缩小的区域重复上述步,直至low>high时,查找失败 查找 88 的过程如下图: 从折半查找过程看,以表的中点为比较对象,并以中点将表分割为两个子表,对定位到的子表继续这种操作。所以,对表中每个数据元素的查找过程,可用二叉树来描述,称这个描述查找过程的二叉树为判定树。 例1:2,5,8,13,25,36,45 小知识: 根据二叉树性质四::n个结点最大的查找次数(成功查找): 所以平均查找次数为: 考试范围:平均比较次数 查找不成功 1.基本思想 分块查找要求将查找表分成若干子表,并对子表建立索引表,查找表的每一个子表由索引表中的索引项确定。 先在索引表中确定要查找的分块,在分块内进行顺序查找。 查找过程:将表分成几块,块内无序,块间有序;先确定待查记录所在块,再在块内查找 适用条件:分块有序表(块内无序,块间有序) 效率在顺序查找和二分查找之间 2.性能分析 由于线性结构插入删除麻烦,所以这里讲树形结构 1.定义: 二叉排序树(Binary Sort Tree)可以 是一棵空树;也可以是具有下列性质的二叉树: ⑴ 若左子树不空,则左子树上所有结点的值均小于根结点的值; ⑵ 若右子树不空,则右子树上所有结点的值均大于根结点的值。 (3) 它的左右子树也都是二叉排序树。 举例:记录的关键码序列为:63,90,70,55,67,42,98,83,10,45,58,则构造一棵二叉排序树的过程如下: 先读入第一个结点作为根,然后读入第二结点,若第二个结点值大于根,则作根的右子树,否则作左子树… 由上图可以看出,对二叉排序树进行中序遍历,便可得到一个按关键码有序的序列:(10,42,45,55,58,63,67,70,83,90,98),因此,一个无序序列,可通过构一棵二叉排序树而成为有序序列。 2.查找算法 解析: 查找成功:走了一条从根到待查结点的一条路径,返回 查找失败:走了一条从根到叶子结点的一条路径,返回t 最大查找长度为二叉排序树的深度,因为比较次数不会超过树的深度。 3.插入算法 由于查找到最后 当一个指针无法完成任务是就用两个指针 4.删除 要求:在查找成功的情况下, 删除这个结点,仍满足二叉排序树。 三种情况: 删除一个叶子: 只需将被删除结点的父结点相应指针域置空。 删除的结点只有一棵子树: 将子树结点替换父结点。 删除的结点左右子树均有: *p=55 PL=42 PR=58然后根据上述定理就可知道删除后图的连法 1.定义 对于一棵非空二叉排序树,它的左子树和右子树都是一棵平衡二叉树,且左子树和右子树的高度之差绝对值不超过 平衡因子:该结点的左子树和右子树高度之差,它的值只能为 2.构造 单向左旋、单向右旋、双向旋转(先左后右)、双向旋转(先右后左) 1 、定义 一棵 (1) 树中每个结点至多有 m 棵子树 ; (2) 根结点至少有两棵子树 ;[2,m] (3) 除根结点之外的非终端结点至少有 (4) 所有叶子结点都出现在同一层次 可用来“查找失败”处理。 答案: 本人博客:https://blog.csdn.net/weixin_46654114 请给我点个赞鼓励我吧
作者:RodmaChen
关注我的csdn博客,更多数据结构与算法知识还在更新
查找表
一.查找
1. 基本概念
据元素。2.衡量一个查找方法

二. 静态查找表
1.顺序表的查找
typedef struct node { DataType data[maxsize];//设置一个一维数组,DataType是元素类型 int length;//实际数量 }sqlist; sqlist L;//定义顺序表 int sqlist_search(sqlist L,Datatype e)//要返回张三的位置,就是一维数组的下标,所以定义的是int类型 { int i=0; While(i<L.length&&L.data[i]!=e)//不能确定循环次数就用while。i<L.length&&L.data[i]!=e没找完且没找到 i++; if(L.data[i]==e) return i;//找到了就返回下标 else return -1;//找完了没找到 } n-i+1次关键码比较,即
Ci=n−i+1。
小妙招;最好的只循环1次,加上最坏循环n次,相加除2。
查找不成功时:ASLsm =(n+1)
为什么加1:比如一个班里面有n个人,问到第n个人的时候还要多问一次,才能确定没有人ASL=((n+1)/2+(n+1))/2= 3 (n+1) / 4
2)优点:算法简单,对表结构无任何要求,关键字是否有序无要求。2.有序表的查找(重点掌握二分查找)
mid =(low + high)/2
low=mid+1high=mid-1


int BinSearch(Sqlist L ,DataType e) { //在表L中查找关键码为e的数据元素,若找到返回该元素在表中的位置,否则返回0 int low=1; high=L.length; //设置初始区间,如果从0开始就定义L。length-1 int mid; while(L.data[mid]!=e&& low<=high) { mid=(low+high)/2; if (e < L.data[mid]) high=mid-1; //调整到左半区 else low=mid+1; //调整到右半区 } if(L.data[mid]==e) return mid; else return 0; }

└ log n ┘ +1 可以求出它的深度 ,最小是1次(└ log n ┘ +1+1)/2ASL=1/7(1+2x2+4x3)=2UNALS=1/8(8x4)=43.索引顺序表的查找 !
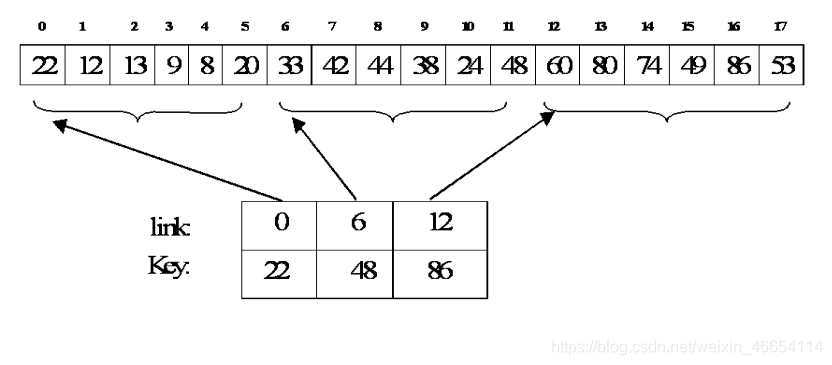
假设:n个数据元素,分成b块,每块有s个数据元素
ASL=2b+1+2s+1=2sn+1+2s+1=21(sn+s)+1
要考! 当s为多少时,ASL最小?
当s=n时,ASL最小,为n+1

三.动态查找表
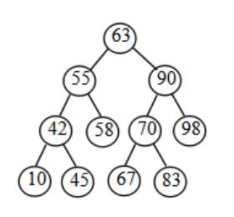
1.二叉排序树(BST)

BiTNode* SearchBST(BiTree T,DataType e)//BiTree T代表根节点。BiTNode*:返回位置*p,指向二叉链表的指针 { BiTNode *p;//工作指针 p=T;//初始值指向根节点 while(p->data!=e&&p!=NULL) { if(e>p->data) p=p->rchild;//向左还是向右 else p=p->lchild; } return p; } t
所指向的结点
(NULL)p为空,无法在使用,所以要设置f指针void InsertBST(BiTree &T, DataType e)//T是根节点 { BiTNode *f, *p; p=*T; while(p!=NULL) { if(p->data==e) return;//如果有这个数值就不需要插入 f=p;//f在父节点 p=((p->data>e)?p=p->lchild:p=p->rchild) }//循环完毕p为空,f为插入的父结点 p=(BiTNode*)malloc(sizeof(BiTNode));//由于p为空没用了,废物利用一下,设置一个空结点 P->data=e; p->lchild=NULL; p->rchild=NULL ;//初始化新结点 if(T==NULL) *T=p;//二级指针:指针自己发生变化。所以前面要设置地址&T else if(p->data>f->data) f->rchild=p; else f->rchild=p; }
PL接替*P成为 *F的子树,PR成为PL最右下结点的右子树(PL表示接结点p的右边left)PR接替*P成为*F的子树,PL成为PR最左下结点的左子树
列:若删除结点55
2.平衡二叉树
1。-1、0、1。
3.B-树(不常考)
m 阶的 B-树,或者是空树,或者是满足下列性质的m 叉树 :
⌈m/2⌉(向上取整) 棵子树 ;[m/2,m]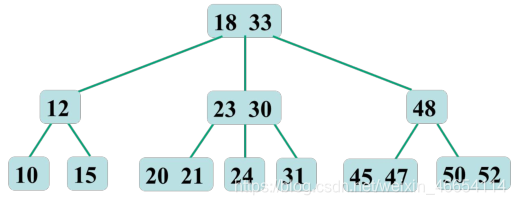
四.边学边练

1)每插入一个结点,从父节点到老祖宗,计算每个结点的平衡因子
2)出现不平衡的点,从他开始画线,画3个,按上述4中类型调整
答案:

本人b站求关注:https://space.bilibili.com/391105864
转载说明:跟我说明,务必注明来源,附带本人博客连接。

本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)