Branin functio is a well-known test function for global optimization. 函数表达式: 函数描述: 1)Dimensions: 2 4)Modifications and Alternate Forms: This rescaled form of the function has a mean of zero and a variance of one. The authors also add a small Gaussian error term to the output. For the purpose of Kriging prediction, Forrester et al. (2008) use a modified form of the Branin-Hoo function, in which they add a term 5×1 to the response. As a result, there are two local minima and only one global minimum, making it more representative of engineering functions. 函数三维图: 函数二维切面:(示意图) References: Forrester, A., Sobester, A., & Keane, A. (2008). Engineering design via surrogate modelling: a practical guide. Wiley. Global Optimization Test Problems. Retrieved June 2013, from Molga, M., & Smutnicki, C. Test functions for optimization needs (2005). Retrieved June 2013, from https://www.zsd.ict.pwr.wroc.pl/files/docs/functions.pdf. Picheny, V., Wagner, T., & Ginsbourger, D. (2012). A benchmark of kriging-based infill criteria for noisy optimization.
f(x)=a(x2−bx12+cx1−r)2+s(1−t)cos(x1)+s
The Branin, or Branin-Hoo, function has three global minima. The recommended values of a, b, c, r, s and t are: a = 1, b = 5.1 ⁄ (4π2), c = 5 ⁄ π, r = 6, s = 10 and t = 1 ⁄ (8π).
2)Input Domain:
This function is usually evaluated on the square x1 ∈ [-5, 10], x2 ∈ [0, 15].
3)Global Minimum:
f(x∗)=0.397887,at,x∗=(−π,12.275),(π,2.275),and(9.42478,2.475)
Picheny et al. (2012) use the following rescaled form of the Branin-Hoo function, on
[0,1]2:
f(x)=51.951[(x2ˉ−4π25.1x1ˉ2+π5x1ˉ−6)2+(10−8π10)cos(x1ˉ)−44.81]
其中,
x1ˉ=15x1−5,x2ˉ=15x2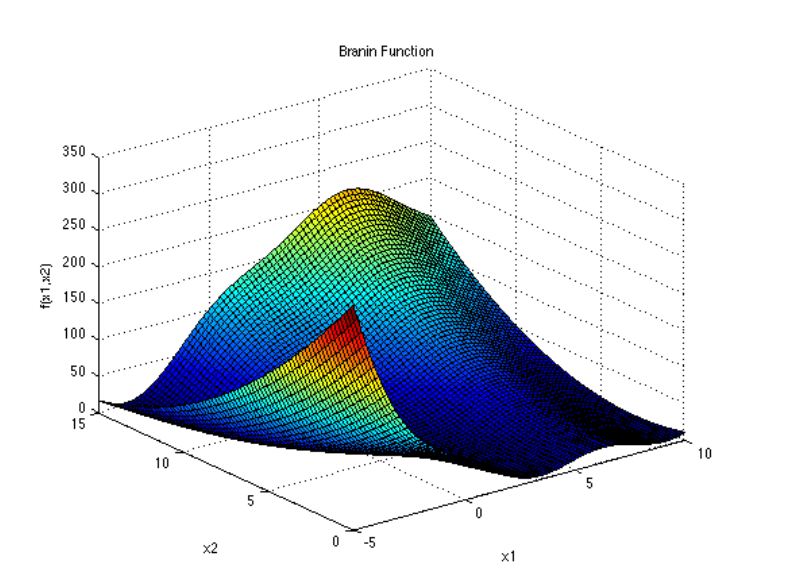
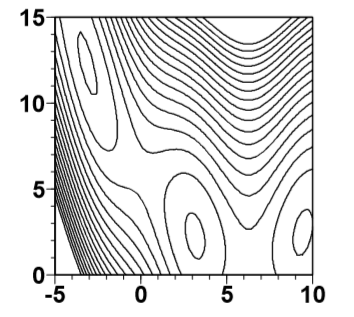
Dixon, L. C. W., & Szego, G. P. (1978). The global optimization problem: an introduction. Towards global optimization, 2, 1-15.
https://www-optima.amp.i.kyoto-u.ac.jp/member/student/hedar/Hedar_files/TestGO.htm.
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)