03 高维组合特征的处理

知识点

• 组合特征

问题 什么是组合特征？如何处理高维组合特征？

分析与解答

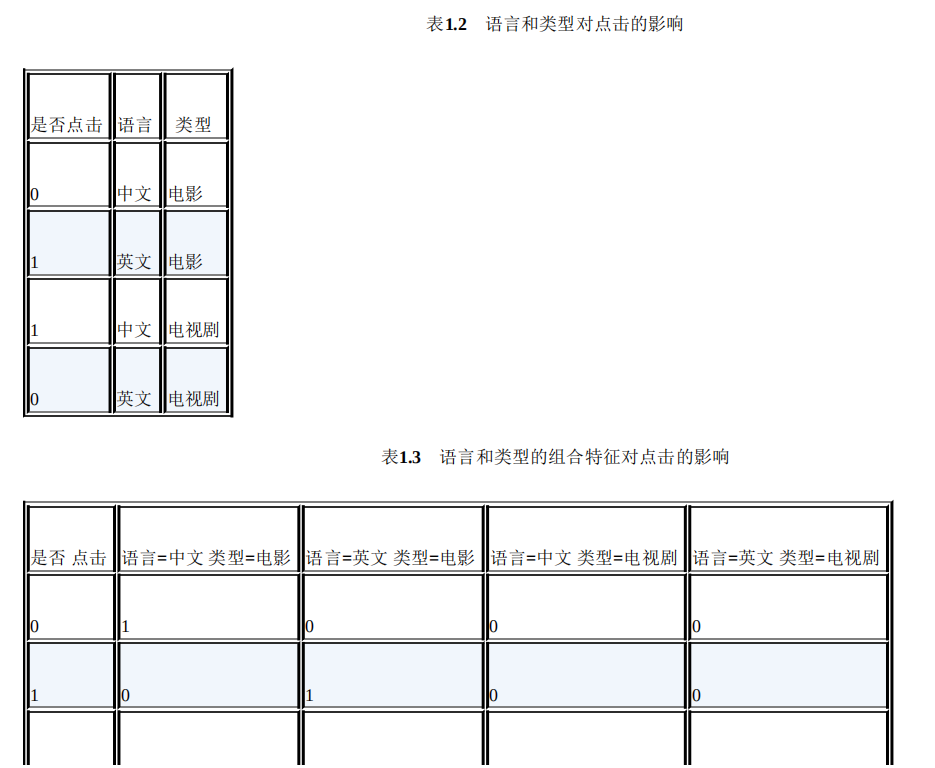
为了提高复杂关系的拟合能力，在特征工程中经常会把一阶离散特征两两组 合，构成高阶组合特征。以广告点击预估问题为例，原始数据有语言和类型两种 离散特征，表1.2是语言和类型对点击的影响。为了提高拟合能力，语言和类型可 以组成二阶特征，表1.3是语言和类型的组合特征对点击的影响。


以逻辑回归为例，假设数据的特征向量为X=(x1,x2,…,xk)，则有，

其中<xi, xj>表示xi和xj的组合特征，wij的维度等于|xi|·|xj|，|xi|和|xj|分别代表第i个特征 和第j个特征不同取值的个数。在表1.3的广告点击预测问题中，w的维度是 2×2=4（语言取值为中文或英文两种、类型的取值为电影或电视剧两种）。这种特 征组合看起来是没有任何问题的，但当引入ID类型的特征时，问题就出现了。以 推荐问题为例，表1.4是用户ID和物品ID对点击的影响，表1.5是用户ID和物品ID的 组合特征对点击的影响。



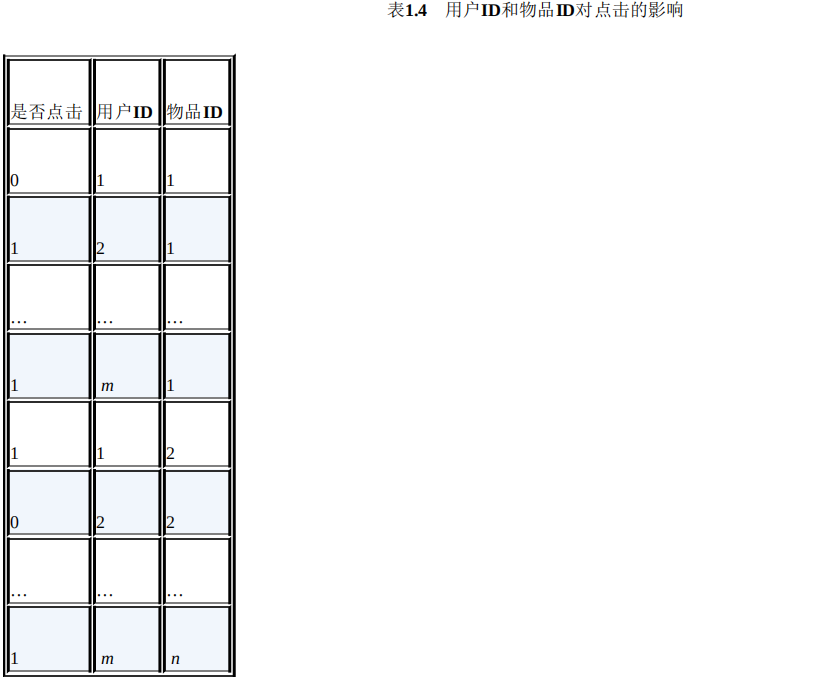
若用户的数量为m、物品的数量为n，那么需要学习的参数的规模为m×n。在 互联网环境下，用户数量和物品数量都可以达到千万量级，几乎无法学习m×n规模 的参数。在这种情况下，一种行之有效的方法是将用户和物品分别用k维的低维向 量表示（k<<m,k<<n），

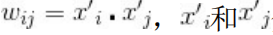其中 ， 分别表示xi和xj对应的低维向量。在表1.5的推荐问题 中，需要学习的参数的规模变为m×k+n×k。熟悉推荐算法的同学很快可以看出来， 这其实等价于矩阵分解。所以，这里也提供了另一个理解推荐系统中矩阵分解的 思路。

另外博主这些年来看过或者听过的一些不错的常用的上千本书籍，没准你想找的书就在这里呢，包含了互联网行业大多数书籍和面试经验题目等等。有人工智能系列（常用深度学习框架TensorFlow、pytorch、keras。NLP、机器学习，深度学习等等），大数据系列(Spark,Hadoop,Scala,kafka等)，程序员必修系列（C、C++、java、数据结构、linux，设计模式、数据库等等）以下是部分截图

更多文章见本原创微信公众号「五角钱的程序员」，我们一起成长，一起学习。一直纯真着，善良着，温情地热爱生活。关注回复【电子书】即可领取哦。

给大家推荐一个Github,上面非常非常多的干货：https://github.com/XiangLinPro/IT_book

When you wake up in the morning, set a goal that today you must be better than yesterday. Do it everyday, grow better!
早上醒来时，给自己定个目标今天一定要比昨天好!每天坚持，一定会大有收获!

2020.6.15于城口