既然你已经打开这篇了,那么我还是想推荐再去看看这一篇: 数据结构(十六) – C语言版 – 树 – 二叉树的线索化及遍历 – 左指针域线索化、顺序表线索化、链表线索化 数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化 上面这个系列已经详细的说明了线索化的方式、代码、遍历等。但是既然提到了线索化,那么还是会很好奇线索化后某个节点的前驱节点、后继节点应该怎么取获取。那么下面就开始说明方法并贴出代码。 首先来一个先序线索化的效果图,如下图所示。 右上图中可以看出来,想要找到某个节点的前驱节点很困难。其中比如: 节点 C 的前驱节点为节点 F ,但是在当前这种二叉链表结构中,我们只有两个指针域( lchild , rchild ),所以我们想单独通过某个节点去查找其前驱节点的话无法确定(无法确定其双亲节点)。 想要实现获取前驱节点,那么可以有两种方式去实现。 第一种:既然需要获取前驱节点,那么在不修改节点的结构的情况下(二叉链表),可以线索成顺序表、双向链表等,那么即可完美满足。那么详细情况可以参考博文: 数据结构(十六) – C语言版 – 树 – 二叉树的线索化及遍历 – 左指针域线索化、顺序表线索化、链表线索化 在二叉链表结构下, 也可以通过一定的方式找到其双其节点,但是确定就是必须要传入树的根节点以及要求双亲节点的节点。所以,在二叉链表的结构下,即使知道其双亲节点也不能完全获取其前驱节点,因为在对某一个节点求取前驱节点的时候,并不知道其所在二叉树的根节点。那么,碎玉某一个节点的双亲节点,可以通过下面的代码获取。 第二种:既然需要确定双亲节点,那么就修改节点的结构,使其节点结构中包含其双亲节点。那么可以将二叉链表转换成三叉链表。三叉链表节点结构定义。 在用三叉链表表示的输的结构下, 创建一个二叉树需要在创建节点的时候将其双亲节点通过参数的形式传入,其创建方式与二叉链表的创建唯二的不同就是: 1、传入参数 — 双亲节点 综上所述,代码可以这样写了。 对于二叉树的线索化,不管是二叉链表还是三叉链表结构形式,都不会有任何改变,因为线索化的过程不涉及到 parent 指针域。详细线索化的的情况可以参考博文。 数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化 上面弄了这么多,不就是为了一个简简单单的前驱节点么。那么根据线序线索化的过程,其前驱节点的特征可以总结为下面这样: 1、如果为根节点,那么前驱节点为空 综上所述,那么代码就可以这样写了。 在先序线索二叉树中查找结点的后继很容易。 如果 lTag == 0 ,说明左指针域为节点的左子树,也就是后继节点 所以,代码就是这么的简单了。 综上所述,在原本二叉链表的形势下,利用 lTag 和 rTag 的标示的形式下的先序线索化,无法在不借助外部力量的情况实现前驱节点的获取,所以说先序线索二叉树是一种不完善的线索化。 首先来一个中序线索化的效果图,如下图所示。 数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化 在中序线索二叉树中查找节点的前驱节点和后继节点都很容易。就像传说中的邻家乖乖女一样。。。。。 按照 中序遍历的顺序(左孩子 -> 根节点 -> 右孩子)来说,某个节点的前驱节点的求取过程可以总结为这样: 1、如果当前节点的 lTag == 1 , 那么其左指针域所指节点即为前驱节点; 所以,代码就是这么的简单了。 按照 中序遍历的顺序(左孩子 -> 根节点 -> 右孩子)来说,某个节点的后继节点的求取过程可以总结为这样: 1、如果当前节点的 rTag == 1 ,那么其右指针域指向即为其后继节点 所以,代码就是这么的简单了。 综上所述,在原本二叉链表的结构下,利用 lTag 和 rTag 的标志的中序线索化,既可以非常方便简单的获取到前驱节点、也可以很容易的得到其后继节点, 所以中序线索二叉树是一种完善的线索化,因此在线索化的领域出现的最为频繁。 首先来一个后序线索化的效果图,如下图所示。 按照 后序遍历的顺序(左孩子 -> 右孩子 -> 根节点)来说,想要获取某个节点的前驱节点,那么也就是获取根节点的右孩子、某个节点的右孩子的某个节点的左孩子…相对而言,前驱节点的获取比较简单…所以某个节点的前驱节点的求取过程可以总结为这样: 1、如果节点的 lTag = 1,那么 lchild 指针域所指即为其前驱节点 所以,代码就可以这么编写了。 前文中我们已经对于后序线索化的后继节点的获取有过简单的描述,并且使用投机取巧的方式完成了在二叉链表的结构下的后序线索化二叉树的遍历。详细的情况请参考博文: 数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化 在不借助外部势力的情况下,我们通过改造自身来实现后继节点的获取后续节点,那么我们就需要将原本的二叉链表修改成三叉链表的结构。具体三叉链表相关内容请点击下列链接查看。 综上所以资料的整合所述,那么后序线索二叉树中查找当前节点的后继节点可以描述为这样: 1、如果当前节点为根节点,则无后继节点 所以,代码就可以这么编写了。 那么既然前面已经说明了三叉链表结构下的后继节点的获取的操作,那么同样的也可以将其遍历弄出来,整体来说呢,线索化后的遍历的过程其实就是一个获取后继节点的过程,所以,在前面后继节点的获取的基础上,我么可以将便利的代码这样写。 当然,求后序线索二叉树中结点的后继要知道其双亲的信息。那么: 1、在三叉链表的结构形式下,我们直接使用其 parent 指针域来获取其双亲节点 综上所述,在原本二叉链表的结构下,利用 lTag 和 rTag 的标志的后序线索化,获取前驱节点比较方便容易,但是想要获取后继节点非常困难,需要知道其双亲节点才能获取到前驱节点,所以需要三叉链表才能完成后继节点的获取。另外,在后续线索化的遍历中,同样需要获取双亲节点,那么在二叉链表的结构下遍历需要借助栈来实现双亲节点的保存。所以后序线索二叉树也是一种不完善的线索化。 关于各种线索化比较详细的总结,可以参考博文: 数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化 下面就是简单总结关于各种方式线索化后的前驱节点、后继节点的特性来说。 1、先序线索二叉树是一种不完善的线索化。 前驱节点:只能使用三叉链表结构,二叉链表结构下的双亲节点也无法获取 2、中序线索二叉树是一种完善的线索化。速度较一般二叉树的遍历速度快,且节约存储空间。 前驱节点:二叉链表结构下即可方便获取,且任意一个节点都能直接找到它的前驱 3、后序线索二叉树也是一种不完善的线索化。 前驱节点:二叉链表结构下可方便获取
内容预览
零、读前说明
一、先序线索化的前驱和后继
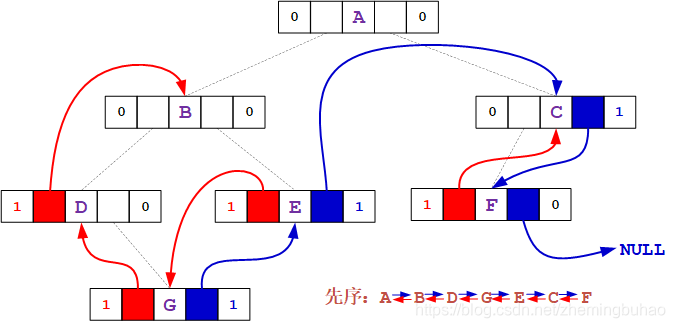
1.1、前驱节点
/** * 功 能: * 先序线索化二叉树的双亲节点 * 参 数: * root :树的根节点 * child:要获取双亲节点的节点 * 返回值: * 成功:child节点双亲节点 * 注意:当child为根节点的时候,返回也是NULL * 失败:NULL **/ BiTNode *prev_thread_parent(BiTNode *root, BiTNode *child) //找孩子的双亲 { BiTNode *ret = NULL; if (root == NULL || child == NULL || root == child) goto END; //这里已经将叶子节点指针域线索化成了前驱和后继,所以得加另外的限制 if ((root->lTag != 1 && root->lchild == child) || (root->rTag != 1 && root->rchild == child)) { ret = root; goto END; } if (root->lTag != 1) //这里同样是要判断是左右孩子还是前驱后继,否则就会造成循环 ret = prev_thread_parent(root->lchild, child); if (ret == NULL && root->rTag != 1) ret = prev_thread_parent(root->rchild, child); END: return ret; } typedef struct BiTNode { TElemType data; /* 节点数据 */ struct BiTNode *lchild; /* 左孩子 */ struct BiTNode *rchild; /* 右孩子 */ struct BiTNode *parent; /* 双亲节点 */ int lTag; int rTag; } BiTNode; 1.1.1、三叉链表下二叉树的创建与线索化
2、将双亲节点赋值与 parent 指针域/** * 功 能: * 创建并且初始二叉树 - 按照先序遍历建立二叉树 * 参 数: * parent : 当前节点的双亲节点 * 返回值: * 成功:创建完成的树的根节点 * 失败:NULL **/ BiTNode *BiTree_Create(BiTNode *parent) { BiTNode *root = NULL; char ch; scanf("%c", &ch); // 如果字符值不为 # ,则说明节点存在 if (ch != '#') { // 为节点申请空间 root = (BiTNode *)malloc(sizeof(BiTNode)); if (root == NULL) return NULL; memset(root, 0, sizeof(BiTNode)); root->parent = parent; // 将字符值赋值给节点 root->data = ch; // 递归创建左孩子,并将返回值赋值给左孩子 root->lchild = BiTree_Create(root); // 递归创建右孩子,并将返回值赋值给右孩子 root->rchild = BiTree_Create(root); } return root; } 1.1.2、三叉链表下前驱节点
2、如果节点的 lTag == 1 ,那么前驱节点为其左指针域所指。
3、如果节点的 lTag == 0 ,那么:
1)如果当前节点为其双亲节点的左孩子,那么其前驱节点为其双亲节点
2)如果当前节点为其双亲节点的右孩子,那么其前驱节点为双亲节点的左子树的第一个右孩子(参考上图中1.1中节点 C 的前驱节点 E。 点我可以查看图1.1。。)。/** * 功 能: * 先序线索化二叉树的前驱节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *prev_thread_prevNode(BiTNode *node) { BiTNode *ret = NULL, *current = node; if (node == NULL) goto END; if (node->parent == NULL) goto END; if (current->lTag == 1) // lTag 为 1,是为官方前驱节点 { ret = current->lchild; } else { BiTNode *pCur = current; // 当前直接的临时保存指针 current = current->parent; if (pCur == current->lchild) // 是双亲节点的左孩子 { ret = current; goto END; } else if (pCur == current->rchild) // 是双亲节点的右孩子 { current = current->lchild; } while (current->rchild == NULL) { if (current->rTag == 0) // 如果rTag = 0,是当前节点的左子树,不然就是后继节点 current = current->lchild; } // 当前节点的右孩子 ret = current->rchild; } END: return ret; } 1.2、后继节点
按照 先序遍历的顺序(根节点 -> 左孩子 -> 右孩子)来说,其后继节点:
如果 rTag == 1 ,说明右指针域为节点的后继节点
如果 rTag == 0 ,说明右指针域为节点的右子树,由于在前面已经判断了左指针域的情况,说明左子树已经访问完毕,所以,右子树即为其后继节点。/** * 功 能: * 先序线索化二叉树的后继节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *prev_thread_nextNode(BiTNode *node) { BiTNode *ret = NULL; if (node == NULL) goto END; if (node->lTag == 0) // 左标志位 0,是为其左孩子,也就是后继节点 { ret = node->lchild; } else // 如果rTag为1,是为正确后继,如果rTag为0,为右孩子 { ret = node->rchild; } END: return ret; } 二、中序线索化的前驱和后继

详细线索化的的情况可以参考博文。2.1、前驱节点
2、如果当前节点的 lTag == 0 ,那么:
1)其左子树不存在右孩子,那么其左子树为其前驱节点
2)其左子树存在右孩子,那么一直找到其最右边的叶子节点,即为前驱节点;/** * 功 能: * 中序线索化二叉树的前驱节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *in_thread_prevNode(BiTNode *root) { BiTNode *ret = NULL; if (root == NULL) goto END; if (root->lTag == 1) // 左标志位 1,可以直接得到前驱节点 { ret = root->lchild; } else // 左标志位0 { ret = root->lchild; while (ret->rTag == 0) // 查找最右下节点的位置 { ret = ret->rchild; } } END: return ret; } 2.2、后继节点
2、如果当前节点的 rTag == 0 ,那么该结点右子树最左边的尾结点就是它的线性后继结点
1)其右子树不存在左孩子,那么其右子树为其后继节点
2)其右子树存在左孩子,那么一直找到其最左边的叶子节点,即为后继节点(其实正好和前驱节点的相反);/** * 功 能: * 中序线索化二叉树的后继节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *in_thread_nextNode(BiTNode *root) { BiTNode *ret = NULL; if (root == NULL) goto END; if (root->rTag == 1) // 右标志位 1,可以直接得到后继节点 { ret = root->rchild; } else // 右标志位0,则要找到右子树最左下角的节点 { ret = root->rchild; while (ret->lTag == 0) // 查找最左下节点的位置 { ret = ret->lchild; } } END: return ret; } 三、后序线索化的前驱和后继

3.1、前驱节点
2、如果节点存在右孩子并且 rTag 不为 1 ,那么 lchild 指针域就是其前驱节点
3、如果节点的 rTag = 0 , 并且同时 rTag = 0 , 那么 lchild 指针域所指就是其前驱节点
4、如果上面的条件都不满足,那么 lchild 指针域所指即为其前驱节点/** * 功 能: * 后序线索化二叉树的前驱节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *post_thread_prevNode(BiTNode *root) { BiTNode *ret = NULL; if (root == NULL) goto END; // 如果 lTag 为 1, 就是本应该的前驱节点 if (root->lTag == 1) ret = root->lchild; // 如果右孩子存在并且 rTag 不为 1, 那么 rchild 指针域就是前驱节点 else if (root->rchild && root->rTag != 1) ret = root->rchild; // 如果 rTag 为 0, 并且同时 rTag 为0, 那么 rchild 指针域就是前驱节点 // 这是因为在左右子树都存在的情况下,不会去进行线索化,但是其节点总归要前驱 // 节点和后继节点的其中一个 else if (root->lTag == 0 && root->rTag == 1) ret = root->lchild; else ret = root->lchild; END: return ret; } 3.2、后继节点
2、如果当前节点为其双亲的右孩子,则其后继节点为其双亲节点
3、如果当前节点为其双亲的左孩子,那么:
1)如果当前节点的双亲节点不存在右孩子,则其双亲节点为其后继节点
2)如果当前节点的双亲节点存在右孩子,则其双亲节点的右子树中按后序遍历的第一个节点为其后继节点。/** * 功 能: * 后序线索化二叉树的后继节点 * 参 数: * root:要查找的节点 * 返回值: * 成功:节点的后继节点 * 失败:NULL **/ BiTNode *post_thread_nextNode(BiTNode *root) { BiTNode *ret = NULL; if (root == NULL) goto END; if (root->rTag == 1) // 官方指定的后继节点 { ret = root->rchild; } else { BiTNode *parent = root->parent; //prev_thread_parent(root); if (parent == NULL) // 根节点,无后继节点 ret = NULL; else if (root == parent->rchild) // 双亲的右孩子,则其后继为其双亲; { ret = parent; } else if (root == parent->lchild && parent->rTag == 1) // 双亲无右子女,则其后继为其双亲; { ret = parent; } else if (root == parent->lchild && parent->rTag == 0) // 双亲有右子女 { root = parent->rchild; // 其双亲的右子树中 按后序遍历的第一个结点。 while (root != NULL && root->lTag == 0) // 要求是左子树 { root = root->lchild; } if (root != NULL && root->rTag == 0) // 说明最左节点还有右孩子 { root = root->rchild; if (root->lTag == 0) // 说明存在左孩子,需要移动到当前左孩子身边 { while (root != NULL && root->lTag == 0) root = root->lchild; } } ret = root; } } END: return ret; } 3.3、三叉链表下的后序线索化的遍历
/** * 功 能: * 遍历线索化二叉树 -- 常规遍历 * 参 数: * root:要遍历的线索二叉树的根节点 * 返回值: * 无 **/ void post_thread_Older_normal(BiTNode *root) { BiTNode *prev = NULL; if (root == NULL) goto END; while (root != NULL) { // 定位到树最左边的节点 while (root->lchild != prev && root->lTag == 0) root = root->lchild; // root->rTag 访问当前节点的后继节点 while (root != NULL && root->rTag == 1) { printf("%c ", root->data); prev = root; root = root->rchild; } // 如果上一次访问记录的节点与当前节点的右孩子重复,则说明当前节点的左子树已经访问完成 while (root != NULL && root->rchild == prev) { printf("%c ", root->data); prev = root; root = root->parent; } // 开始遍历右子树 if (root != NULL && root->rTag == 0) { root = root->rchild; if (root->lTag == 0) // 说明存在左孩子,需要移动到当前左孩子身边 { while (root != NULL && root->lTag == 0) root = root->lchild; } } } END: printf("n"); return; }
2、在二叉链表的结构形式下,我们可以通过 栈 的特性来保存当前节点的双亲节点四、总结
后继节点:二叉链表结构下可相对容易获取
后继节点:二叉链表结构下即可方便获取,且任意一个节点都能直接找到它的后继
后继节点:二叉链表结构下需要借助 栈 模型,且其双亲节点也无法获取。使用三叉链表结构可以获取
好啦,废话不多说,总结写作不易,如果你喜欢这篇文章或者对你有用,请动动你发财的小手手帮忙点个赞,当然关注一波那就更好了,好啦,就到这儿了,么么哒(*  ̄3)(ε ̄ *)。

上一篇:数据结构(十七) – C语言版 – 树 – 二叉树的线索化及遍历 – 先序线索化、中序线索化、后序线索化
下一篇:数据结构(十九) – C语言版 – 树 – 树、森林、二叉树的江湖爱恨情仇、相互转换
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)