建议先看上一篇基本概念篇 https://blog.csdn.net/weixin_45755332/article/details/106899147 树:没有圈的连通图 最小生成树问题:在一个赋权的连通的无向图 G 中找出一个生成树,并使得这个生成树的所有边的权数之和为最小。 最小生成树的常用方法: 下面用代码来解下面最小生成树 下面用避圈算法的MATLAB程序计算上题,结果一样 某大学准备对其所属的7各学院办公室计算机联网,这个网络的可能联通的途径如图11- -14所示,图中V1,——,V7表示7个学院办公室,图中的边为可能联网的途径,边上所赋的权数为这条路线的长度,单位为百米。请设计一个网络能联通7个学院办公室,并使总的线路长度为最短。 最大流问题(maximum flow problem),一种组合最优化问题,就是要讨论如何充分利用装置的能力,使得运输的流量最大,以取得最好的效果。 第一步: 找出第一个可行流,例如所有弧的流量fij =0; 第二步:对点进行标号找一条增广链。 第三步:调整流量 定理1 可行流f是最大流的充分必要条件是不存在发点到收点的增广链 . 例 求图中的发点v1到收点v7的最大流. 增广链μ={(1,2),(3,2),(3,4),(4,7) },μ+={(1,2),(3,4),(4,7)},μ-={(3,2)},调整量为增广链上点标号的最小值 θ=min{∞,2,3,3,7}=2,对其进行调整 将图G=(V,E)的点集分割成两部分 下图所示的截集为 为什么没有{2,3}呢?是因为弧内的① ③ 要指向弧外的 ② ④ ⑤ ⑥ ,{2,3}是弧外的指向弧内的了。
最小生成树
基本概念和方法
图一是,图二有圈,图三灭有连通



生成子图:对于无向图 G =(V,E) ,保留G的所有点,而删掉G的边或者保留部分 G 的边,所获得的图称为 G 的生成子图。
如左图去了那两条边,剩下的那个图就是生成子图


生成树:若图 G 的一个生成子图是一个树,则称这个生成子图为生成树。上面右图就是一个最小生成树


2. 加边法(避圈法):2.加边法(避圈法) :取图G的n个孤立点{v1,v2,…, vn}作为一个支撑图,从最短边开始往支撑图中添加,见圈回避,直到连通(有n-1条边)


连接完第四条线时,v1→v2和v3→v6权值都是5,但v1→v2连接的话就是圈了,所以只能是v3→v6
设置两个集合P和Q,其中P用于存放的最小生成树G中的顶点,集合Q存放的最小生成树G中的边。令集合P的初值为
P=v1 (假设构造最小生成树时从顶点
v1 出发),集合Q的初值为
Q=θ 。
prim算法的思想是,从所有
p∈P,v∈V−P ,的边中,选取具有最小权值的边 pv ,将顶点v加入集合P中,将边pv加入集合Q中,如此不断重复,直到 P=V 时,最小生成树构造完毕,这时集合Q中包含了最小生成树的所有边。
用result 3*n 的第一、二、三行分别表示生成树边的起点、终点、权集合。

clc;clear; a=zeros(7); a(1,2)=50; a(1,3)=60; a(2,4)=65; a(2,5)=40; a(3,4)=52;a(3,7)=45; a(4,5)=50; a(4,6)=30;a(4,7)=42; a(5,6)=70; a=a+a';a(a==0)=inf; result=[];p=1;tb=2:length(a); while size(result,2)~=length(a)-1 temp=a(p,tb);temp=temp(:); d=min(temp); [jb,kb]=find(a(p,tb)==d,1); %找第1个最小值 j=p(jb);k=tb(kb); result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[]; end result result = 1 2 5 4 4 7 2 5 4 6 7 3 50 40 50 30 42 45 clc;clear; a(1,[2,3])=[50,60]; a(2,[4,5])=[65,40]; %这里给出邻接矩阵的另外一种输入方式 a(3,[4,7])=[52,45]; a(4,[5,6])=[50,30]; a(4,7)=42; a(5,6)=70; [i,j,b]=find(a); data=[i';j';b'];index=data(1:2,:); loop=length(a)-1; result=[]; while length(result)<loop temp=min(data(3,:)); flag=find(data(3,:)==temp); flag=flag(1); v1=index(1,flag);v2=index(2,flag); if v1~=v2 result=[result,data(:,flag)]; end index(find(index==v2))=v1; data(:,flag)=[]; index(:,flag)=[]; end result result = 4 2 4 3 1 4 6 5 7 7 2 5 30 40 42 45 50 50

注:这是一个最小生成树问题,不是最短路问题,因为他所有的都要连接上。clc;clear; a=zeros(7); a(1,7)=3; a(1,6)=10; a(2,7)=3; a(2,3)=1; a(3,4)=7; a(3,5)=2;a(3,7)=4; a(4,5)=8; a(5,6)=4; a(5,7)=5; a(6,7)=3; a=a+a';a(a==0)=inf; result=[];p=1;tb=2:length(a); while size(result,2)~=length(a)-1 temp=a(p,tb);temp=temp(:); d=min(temp); [jb,kb]=find(a(p,tb)==d,1); %找第1个最小值 j=p(jb);k=tb(kb); result=[result,[j;k;d]];p=[p,k];tb(find(tb==k))=[ ]; end result result = 1 7 2 3 7 3 7 2 3 5 6 4 3 3 1 2 3 7 最大流问题
基本概念
如图所示的网络图中定义了一个发点v1,定义了一个收点v7,其余点v2,v3,…,v6为中间点,称为转运点。如果有多个发点和收点,则虚设发点和收点转化成一个发点和收点。图中的权是该弧在单位时间内的最大通过能力,称为弧的容量(capacity)。最大流问题是在单位时间内安排一个运送方案,将发点的物质沿着弧的方向运送到收点,使总运输量最大。

设
cij为弧(i,j)的容量,
fij为弧(i,j)的流量。
容量是弧(i,j)单位时间内的最大通过能力,流量是弧(i,j)单位时间内的实际通过量,流量的集合
f=fij称为网络的流。发点到收点的总流量记为v=val(f),v也是网络的流量。
注意:流量只是发出点的发出量或流入点的流入量,中间点的流入量和流出量是一样的。
概念区分
链:从发点到收点的一条路线(弧的方向不一定都同向)称为链。从发点到收点的方向规定为链的方向。
前向弧:与链的方向相同的弧称为前向弧。
后向弧:与链的方向相反的弧称为后向弧。
增广链: 设 f 是一个可行流,如果存在一条从vs到vt的链,满足:
1.所有前向弧上
fij<Cij
2.所有后向弧上fij>0

Ford-Fulkerson标号算法
vi 已标号并且另一端未标号的弧沿着某条链向收点检查:
cij<fij,则vj标号:
θj=cij-fij(容量−流量)
fji>0,则vj标号:
θj=fji
当收点已得到标号时,说明已找到增广链,依据vi 的标号反向跟踪得到一条增广链。当收点不能得到标号时,说明不存在增广链,计算结束。
θ=minjθj
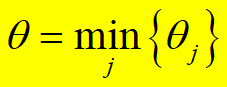
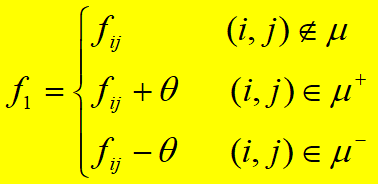
得到新的可行流f1,去掉所有标号,返回到第二步从发点重新标号寻找增广链,直到收点不能标号为止.

先假设已经给定了这个可行流,可以检查一下,发点和接收点的流量是相同的,都是16;每个点的流入量和流出量也是相同的。
然后进行第一轮标号
1→2}正向弧,8-6=2,圈2上就标号为2;
2→4}{
2→6}都是正向弧,但流量已经到达最大流了,所以不能增加了
2→5}反向弧,所以圈3直接标3-0=3
3→4}正向弧,圈4标3,当然也可以{3→6→4}这样多一条路径但结果一样就不用这个了
这里有反向弧,调整后是正向弧+2,反向弧-2

第二轮
与第一轮是一样的,要说的就是{3→2}虽然没有到最大容量,但圈2往后不能增加了,所以直接不用看

增广链μ=μ+={(1,3),(3,4),(4,7) },调整量为 θ=min{∞,4,1,5}=1
这里没有反向弧,经过的弧流量都加1

第三轮

增广链μ=μ+={(1,3),(3,6),(6,4),(4,7) },调整量为 θ=min{∞,3,1,2,4}=1
全是正向弧,都加1

经过排查只有这些增广链了,所以可以下结论了
最大流量
v=f12+f13=8+12=20=f67+f47+f57=6+2+7+7
上面是有向图,无向图就更简单了,直接全是加就完了。截集-截量法
V1,V1并且
vs∈V1以及
vt∈V1,则箭尾在V_1箭头在
V1 的弧集
V1,V1称为一个截集,截集中所有弧的容量之和称为截集的截量。
V1,V1={(1,2),(3,4),(3,5)},截量C=6+2+2=10;

又如下图所示的截集为
V1,V1= {(2,4),(3,(5,4)(5,0)}
截量
C(V1,V1)=4+2+6+9=21
下图所示的截集为
V1,V1= {(2,4),(2,5),(3,4),(3,5)}
截量C=4+1+2+2=9

所有截量中此截量最小且等于最大流量,此截集称为最小截集。经过计算这个图最小截量就是9,所以最大流量就是9;
定理2最大流量等于最小截集的截量。
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)