导言

pid在工业上的应用占90%以上。但许多没学过自动控制原理的小伙伴着实难以理解，所以我在这里尽我所能，用简单的高数知识给大家讲一些我自己的理解。由于pid在网上有许多可参考的资料，我这里重点分析pid控制器的稳态误差，这是我当时学习时最难理解的地方。据我所知，在其他对pid的介绍里几乎没有过对这方面的详细解释。所以我这里小谈一番。
如想深入了解pid控制器的原理，可参考自动控制原理。（根轨迹法最容易理解，如不必要，可只看时域法与根轨迹法）
本文只针对单位反馈的系统。
本文属个人理解，可能缺乏严谨性

基础知识

• 微分算子
  记
  $frac{d}{dt}=s$

  dtd​=s，则
  $int_{}^{} , dx=frac{1}{s}$

  ∫​dx=s1​。
  s即被称为微分算子。

• 算子表示微分方程
  微分方程
  $ddot{y}+3dot{y}+2y=x$

  y¨​+3y˙​+2y=x。
  用算子表示
  $s^2y+3sy+2y=x$

  s2y+3sy+2y=x。
  则
  $frac{y}{x}=frac{1}{s^2+3s+2}$

  xy​=s2+3s+21​，该式子表示了y与x的关系，即自控中的传递函数。

PID的公式推导

y为输出，x为输入。p,i,d分别为比例，积分，微分系数

$y=p*error(t)+i*int_{}^{},error(t)dt+d*error'(t)$

y=p∗error(t)+i∗∫​error(t)dt+d∗error′(t)

$y=p(x-y)+i*int_{}^{},(x-y)dt+d(x’-y’)$

y=p(x−y)+i∗∫​(x−y)dt+d(x′−y′)

$y=p(x-y)+frac{i}{s}(x-y)+ds(x-y)$

y=p(x−y)+si​(x−y)+ds(x−y)
移向后，分离x，y，化简，则可求出输出与输入的关系
$frac{y}{x}=frac{ds^2+ps+i}{ds^2+（p+1）s+i}$

xy​=ds2+（p+1）s+ids2+ps+i​

PID的误差分析

• P控制器：快速抵消干扰
  让i和d等于0，则
  $frac{y}{x}=frac{p}{p+1}$

  xy​=p+1p​。由上式可以看出，输入与输出是纯比例的关系，最终稳态时，输出
  $y=frac{xp}{1+p}$

  y=1+pxp​，则误差很容易算出
  $error=x-y=frac{x}{1+p}$

  error=x−y=1+px​，所以，但用p控制器必然存在误差，增大p可减小误差，但会降低系统的稳定性。仿真结果：
  

• PI控制器：消除p控制器的稳态误差(积分消除误差)
  即让d=0，则
  $frac{y}{x}=frac{ps+i}{（p+1）s+i}$

  xy​=（p+1）s+ips+i​。因为s代表微分算子，微分乘以常数即为0。观察上式，在稳态时（s的一次及多次项为0），
  $frac{y}{x}=frac{i}{i}=1$

  xy​=ii​=1，即
  $x-y=0$

  x−y=0,无稳态误差。所以pi控制器无稳态误差和=，但如果i过大，同样不利于系统的稳定。仿真结果：
  

• PD控制器：提高系统快速性(微分可超前预测)
  即让i=0，则
  $frac{y}{x}=frac{ds+p}{ds+p+1}$

  xy​=ds+p+1ds+p​同上述方法，可算出pd控制器的稳态误差为
  $frac{xp}{1+p}$

  1+pxp​由于d控制器具有前瞻性，所以可适当调大p以减小稳态误差。故pd控制器提高了系统快速性，也减小了稳态误差，但稳态误差不能为0。仿真结果：
  

• PID控制器
  pid控制器即集合了i与d控制器的综合效果。消除了稳态误差的同时，又提高了快速性与响应能力。仿真结果：
  
  代码实现：
  

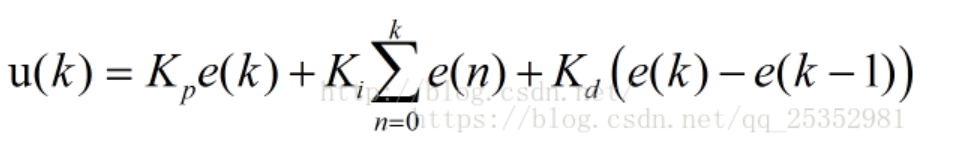
结语

至于pid调参等内容也是很重要的，推荐大家利用matlab仿真，有助于理解。给出matlab代码：

clear,clc; out=zeros(1,1000); p=0.5; i=0.0; d=0.0; error=zeros(1,2); pout=0; iout=0; dout=0; target=20; for t=2:1000;     error(2) = error(1);     error(1) = target - out(t-1);          pout = p(1) * error(1);     iout = iout + i(1)* error(1);     dout= d(1) * ( error(1) - error(2));          out(t) = pout + iout + dout;      end tt=1:1000; plot(tt,out);