虽然做出的题比较多,但是排名一次比一次差,主要今天什么题都wa好几发,在罚时上没有一点优势可言。 题意:4种类型的场景, 0:没有鱼、没有诱饵,但是可以消耗一个诱饵钓一条鱼。 1:没有鱼 有诱饵,此时你可以旋转诱饵,使得自己诱饵数量++。 2:有一条 鱼 没有诱饵,此时你可以不消耗诱饵免费得到一条鱼 3:即有鱼又有诱饵,你可以选择一个。 问如果有n种以上场景,如果操作使得自己的鱼最多。 做法:这题本来想拿拿一血,结果慢了16s。。。。 这类题很明显的情况遇到2、3就尽量拿鱼。遇到1 只能 钓鱼。遇到3 是选择钓鱼呢?还是选择诱饵。 想起一道cf的D题:给你n个棍子,构造1(两根)、2(五根)、3(五根)、4(4根)、5、6、7、8、9。类似于电子表上的显示,消耗棍子,问最大能构造多大的数。忘记是哪场的了。 这类题 主要是看当前构造对后续的构造是否有影响。 那么此题 就是倒着求后缀能钓鱼的场景(1,2) ,从前面枚举的时候,如果诱饵数小于后缀能钓鱼的场景数,那就选择诱饵,否则选择钓鱼。 签到题 题意:给定20个坐标值(可能顺时针,可能逆时针),问你点构成的图 是右手还是左手。 此图是右手(题目保证,手的大小不变)。 做法:这么个简单题,队友n方求两点之间的距离,然后稀奇古怪的什么判断 给我贡献了 5发罚时(微笑) 用叉积判断顺时针还是逆时针,然后判断 6、9、8的顺序即可。 比较的坑的比方是,这里判断是否相等的esp 得是1e-4 1e-5wa了,原理不懂。 题意: 可以转换为 两两坐标配对,对答案得贡献就一对之间的值之差的绝对值。要求构造出两种情况,n保证为偶数 做法:第一种:1-2 3-4 5-6。 第二种,在不包含第一种的情况下dp。 dp[i]代表前i个全部配对好。要想贡献值最小,很明显要使得配对的两个值差最小,对a排序后dp。 三种情况: 题意: 做法:参考来自官方题解。 证明每太看懂。 于是搜博客:博客 懂了。 代码: 题意:n个点 m条边的图。每个点 最初属于自己的集合。q次操作,每次操作把 x 附近连边的点 加入到x的集合。若之前x已经加入到其他集合了,那么此次操作无效 做法:并查集 + 按秩合并,感觉是一个比较简单的题。是队友写的,就贴队友代码了。 对每个点维护属于自己的外围点 队列。每次操作就从x的外围点进行一次外层扩展合并。对于每个点属于哪个集合,就用并查集维护公共的父亲节点就好了
A-Clam and Fish
#include<bits/stdc++.h> #define rep(i,a,b) for(int i=a;i<=(b);++i) #define per(i,a,b) for(int i=a;i>=(b);--i) #define mem(a,x) memset(a,x,sizeof(a)) #define pb emplace_back #define pii pair<int,int> #define mk make_pair using namespace std; typedef long long ll; ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;} inline ll read() { ll x=0,w=1; char c=getchar(); while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();} while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();} return w==1?x:-x; } const int N=2e6+10; char s[N]; int n,dp[N]; int main() { int _=read();while(_--) { n=read(); rep(i,1,n+1) dp[i]=0; scanf("%s",s+1); int ans=0,num=0; for(int i=n;i>=1;--i){ dp[i]=dp[i+1]; if(s[i]=='0'||s[i]=='1') dp[i]++; } rep(i,1,n){ if(s[i]=='0'){ if(num) ans++,num--; } else if(s[i]=='1') { if(num<dp[i+1]) num++; else { if(num) num--,ans++; } } else if(s[i]=='2') ans++; else ans++; } printf("%dn",ans); } }B-Classical String Problem
#include<bits/stdc++.h> #define rep(i,a,b) for(int i=a;i<=(b);++i) #define per(i,a,b) for(int i=a;i>=(b);--i) #define mem(a,x) memset(a,x,sizeof(a)) #define pb emplace_back #define pii pair<int,int> #define mk make_pair using namespace std; typedef long long ll; ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;} inline ll read() { ll x=0,w=1; char c=getchar(); while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();} while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();} return w==1?x:-x; } const int N=2e6+10; char s[N]; int n,now; int main() { scanf("%s",s); n=strlen(s); int now=0; int q=read();while(q--){ char ty[2];int x; scanf("%s%d",ty,&x); //printf("now:%d x:%dn",now,x); if(ty[0]=='A'){ printf("%cn",s[(now+x-1+n)%n]); } else{ if(x>0){ now=(now+x)%n; } else{ now=(now+x)%n; } //printf("now:%dn",now); } } }C-Operation Love
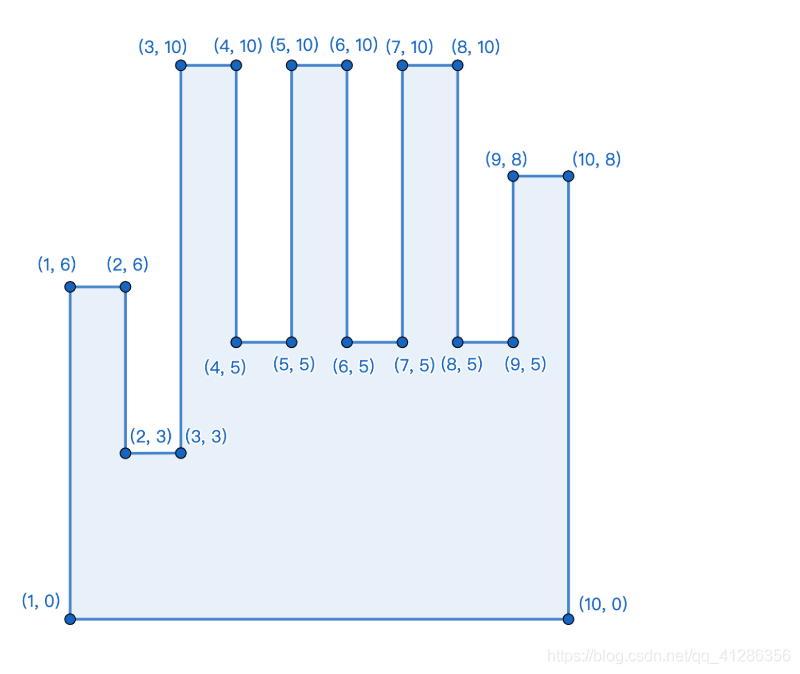
#include<bits/stdc++.h> using namespace std; const int N=30; struct Point{ double x,y; }p[N]; int n; double polygonarea() { int i,j; double area = 0; for(i = 0;i < n;++i){ j = (i+1)%n; area += p[i].x*p[j].y; area -= p[i].y*p[j].x; } //area /= 2.0; return area; } double run(int id,int id2) { id=id%n; id2=id2%n; return (p[id].x-p[id2].x)*(p[id].x-p[id2].x)+(p[id].y-p[id2].y)*(p[id].y-p[id2].y); } double cmp(double a,double b) { if(abs(a-b)<1e-4) return 1; return 0; } void solve() { string ans1="right",ans2="left"; if(polygonarea()<0){ swap(ans1,ans2); } for(int i=0;i<n;++i){ if(cmp(run(i,i+1),36)&&cmp(run(i+1,i+2),81)&&cmp(run(i+2,i+3),64)){ cout<<ans1<<endl; return ; } if(cmp(run(i,i+1),64)&&cmp(run(i+1,i+2),81)&&cmp(run(i+2,i+3),36)){ cout<<ans2<<endl; return ; } } } int main() { n=20; int _;scanf("%d",&_);while(_--) { for(int i=0;i<n;++i) cin>>p[i].x>>p[i].y; solve(); } }E-Two Matchings

if(i%2==0) { dp[i]=min(dp[i],dp[i-4]+a[i]-a[i-3]+a[i-1]-a[i-2]); dp[i]=min(dp[i],dp[i-4]+a[i]-a[i-2]+a[i-1]-a[i-3]); if(i-5>=1){ dp[i]=min(dp[i],dp[i-6]+a[i]-a[i-2]+a[i-1]-a[i-4]+a[i-3]-a[i-5]); } }
#include<bits/stdc++.h> #define rep(i,a,b) for(int i=a;i<=(b);++i) #define per(i,a,b) for(int i=a;i>=(b);--i) #define mem(a,x) memset(a,x,sizeof(a)) #define pb emplace_back #define pii pair<int,int> #define mk make_pair using namespace std; typedef long long ll; ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;} inline ll read() { ll x=0,w=1; char c=getchar(); while(c<'0'||c>'9') {if(c=='-') w=-1; c=getchar();} while(c<='9'&&c>='0') {x=(x<<1)+(x<<3)+c-'0'; c=getchar();} return w==1?x:-x; } const int N=2e6+10; ll a[N],dp[N]; int n; int main() { int _=read();while(_--) { n=read(); rep(i,1,n) a[i]=read(); rep(i,0,n+1) dp[i]=1e18; sort(a+1,a+1+n); //rep(i,0,3) dp[i]=0; dp[0]=0; rep(i,4,n){ if(i%2==0) { dp[i]=min(dp[i],dp[i-4]+a[i]-a[i-3]+a[i-1]-a[i-2]); dp[i]=min(dp[i],dp[i-4]+a[i]-a[i-2]+a[i-1]-a[i-3]); if(i-5>=1){ dp[i]=min(dp[i],dp[i-6]+a[i]-a[i-2]+a[i-1]-a[i-4]+a[i-3]-a[i-5]); } } } // rep(i,1,n){ // printf("%lldn",dp[i]); // } ll res = 0; for(int i=1;i<=n;i+=2) res+=a[i+1]-a[i]; //ll ans=min({(a[n]-a[1])*2,run1(),run2(),run3(),run4(),run5()}); printf("%lldn",dp[n]+res); } }F-Fraction Construction Problem




#include <bits/stdc++.h> using namespace std; typedef long long ll; #define mem(a,b) memset(a , b , sizeof(a)) const int N = 5e6 + 10; int prime[N],p; bool is_prime[N]; void init() { for(int i=2;i<N;++i){ if(!is_prime[i]) prime[++p]=i; for(int j=1;j<=p&&prime[j]*i<N;++j){ is_prime[prime[j]*i]=1; if(i%prime[j]==0) break; } } } ll gcd(ll a, ll b) { return b == 0 ? a : gcd(b, a % b); } ll ex_gcd(ll a, ll b, ll &x, ll &y) { ll res, t; if(!b) { x = 1; y = 0; return a; } res = ex_gcd(b, a % b, x, y); t = x; x = y; y = t - (a / b) * y; return res; } ll solve_ex_gcd(ll a, ll b, ll c, ll &x, ll &y) { ll inv = ex_gcd(a, b, x, y); if(c % inv) { x = -1; y = -1; return -1; } x *= (c / inv); y *= (c / inv); return 0; } void solve() { ll a, b; cin >> a >> b; ll k = gcd(a, b); if(k != 1) { a /= k;b /= k; printf("%lld %lld %lld %lldn",a+1,b,1,b); return ; } if(b == 1 || is_prime[b]==0) puts("-1 -1 -1 -1"); else { ll tmp = 0, time = 0; ll bb = b; for(int i = 1;i <= p && bb != 1; i++) // 找两个素因数 { if(bb % prime[i] == 0) { tmp = prime[i]; while(bb % prime[i] == 0) time++,bb /= prime[i]; break; } } if(bb == 1){puts("-1 -1 -1 -1");return ;} ll d = 1; for(int i = 1;i <= time; i++) d *= tmp; // b的一个因数 ll f = bb; // b的另一个因数 ll c = 0, e = 0; solve_ex_gcd(f, d, a, c, e); if(c < 0 && e > 0) cout << e << " " << f << " " << -c << " " << d << endl; else cout << c << " " << d << " " << -e << " " << f << endl; } } int main() { init(); int _;scanf("%d",&_);while(_--) solve(); } G-Operating on a Graph
#include <bits/stdc++.h> using namespace std; #define ll long long ll input(){ ll x=0,f=0;char ch=getchar(); while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar(); while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); return f? -x:x; } #define pb push_back const int N=8e5+1; struct node{ int w; node *next; }; struct Qu{ node *head,*end,*del; int front(){ return head->w; } void push(int x){ if(head==NULL&&end==NULL) head=end=new(node); else{ end->next=new(node); end=end->next; } end->w=x; } void pop(){ del=head; if(head==end) head=end=NULL; else head=head->next; delete(del); } bool empty(){ return head==NULL&&end==NULL; } }q[N]; int fa[N],rk[N]; int find(int x){ return fa[x]==x? x:(fa[x]=find(fa[x]));} void merge(int x,int y){ x=find(x),y=find(y); if(x!=y){ if(rk[x]>=rk[y]){ while(!q[y].empty()) q[x].push(q[y].front()),q[y].pop(); fa[y]=x,rk[x]+=rk[y]; }else{ while(!q[x].empty()) q[y].push(q[x].front()),q[x].pop(); fa[x]=y,rk[y]+=rk[x]; } } } vector <int> G[N]; Qu tmp; map <int,int> mp; int n,m; void Solve(){ n=input(),m=input(); mp.clear(); for(int i=1;i<=n;i++){ while(!q[i].empty()) q[i].pop();q[i].push(i); rk[i]=1,fa[i]=i;G[i].clear(); mp[i]=i; } for(int i=1;i<=m;i++){ int u=input()+1,v=input()+1; G[u].pb(v),G[v].pb(u); } int QQ=input(); for(int i=1;i<=QQ;i++){ while(!tmp.empty()) tmp.pop(); int u=input()+1,tu; tu=u; if(u!=mp[find(u)]) continue; u=find(u); while(!q[u].empty()) tmp.push(q[u].front()),q[u].pop(); // cout<<i<<":"<<tmp.front()<<endl; while(!tmp.empty()){ int t=tmp.front();tmp.pop(); for(auto v:G[t]){ merge(v,t); } } mp[find(u)]=tu; } for(int i=1;i<=n;i++){ printf("%d%c",mp[find(i)]-1,i==n? 'n':' '); } } int main(){ int T=input(); while(T--) Solve(); }
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)