在前面遍历二叉树的操作里,基本上都是使用递归实现的,因为递归解决问题的方式会相对循环来说要更加简单一些。但是我们要知道,对于计算机而言,却未必如此。 递归的优点,想必在之前也已经体会到了。使用递归解决问题,往往思路清晰,简单易懂。但是我们要知道,递归在调用的时候会占用大量的系统堆栈,内存耗用非常的多。在递归调用层次多的时候,速度也要比循环慢得多。所以说,在要求高性能的情况下尽量避免使用递归,递归调用既花时间又耗内存。 我们可以由用户自己定义一个栈来代替系统栈,也就是用非递归的方式来实现遍历算法,这样一来可以得到不小的效率提升。 那么问题来了。一个是系统栈,而另一个是用户定义的栈。明明都是栈,为什么用户定义的栈会比系统的栈更高效? 这里的一个解释是递归函数所申请的系统栈,是一个所有递归函数都通用的栈。对于二叉树深度优先遍历算法。系统栈除了记录访问过的结点信息之外,还有其它信息需要记录,以实现函数递归的调用。而用户自己定义的栈,仅保存了遍历所需的节点信息,是对遍历算法的一个针对性的设计,对于遍历算法来说,显然要比递归函数通用的系统栈更高效。 中序遍历和前序遍历差不多。遍历到左孩子最底层之前的结点都会先存入栈内,等遍历到了左孩子最底层结点之后,才会开始出栈进栈的过程。 在后序遍历操作之前,我们可以先手动写上遍历的结果再进行过程分析 刚才的先序遍历结果为: A B D H I E J K C F G 后序遍历的结果为: H I D J K E B F G C A 后序遍历逆转的结果:A C G F B E K J D I H 我们仔细观察会发现一个规律。就是当我们把后序遍历的结果倒过来之后就比较像是先序遍历过程中的左右子树顺序交换后的结果。所以,我们只需要将前面的先序遍历算法中的左右子树顺序交换就可以得到逆转后的后序遍历序列。然后再把逆转后的序列逆序也就得到了我们想要的结果。这么做的话,我们就需要两个栈。 一个栈用来辅助做逆后序遍历,然后将遍历结果的序列压入另一个栈当中。由于栈是先进后出的数据结构,所以只需要按照栈的顺序把它们正常出栈。就得到我们想要的结果了~
使用自定义的栈来优化二叉树的遍历
本文是上一篇文章的后续,详情点击该链接~
前言
递归的缺点
优化方案
代码实现
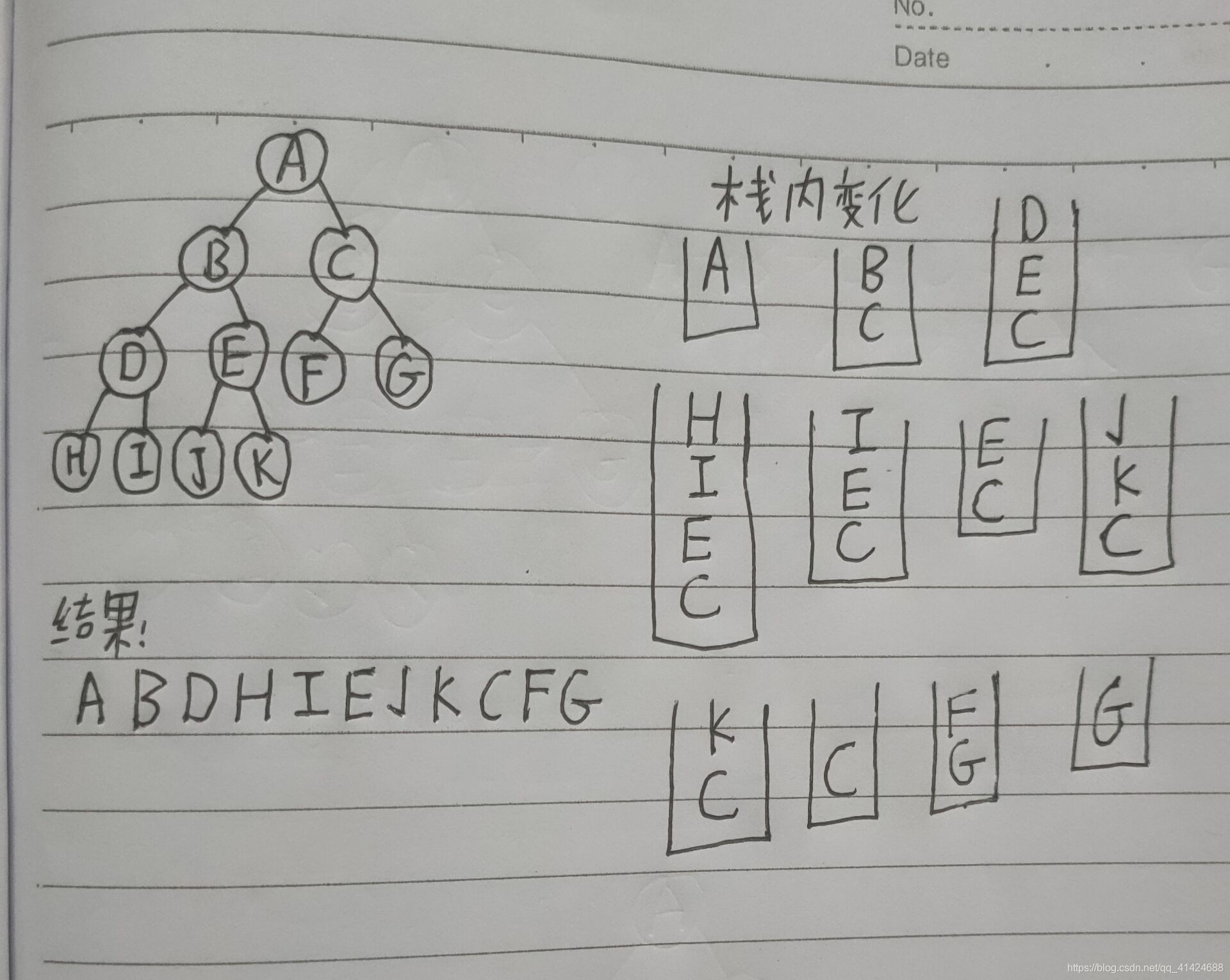
二叉树的结构还是继续使用上篇文章开头图片上的那棵树。
先序遍历
void preOrder(Tree *btn) { if (btn != NULL) { //定义一个栈 Tree* Stack[MAXSIZE]; //初始化栈 int top = -1; Tree* p; //根节点入栈 Stack[++top] = btn; //栈空循环退出,遍历结束 while (top != -1) { //出栈并输出栈顶结点 p = Stack[top--]; printf("%c ",p->data); //栈是先进后出的,所以先让右孩子进去,再进左孩子 //等下出来的时候.就是左孩子先出来,右孩子后出来 //栈顶结点的右孩子存在,则右孩子入栈 if (p->right != NULL) { Stack[++top] = p->right; } //栈顶结点的左孩子存在,则左孩子入栈 if (p->left != NULL) { Stack[++top] = p->left; } } } } 我们看到,运行的结果和刚才用笔在本子上分析的一样
中序遍历
void InOrder(Tree *tree) { if (tree != NULL) { Tree* Stack[MAXSIZE]; int top = -1; Tree* p; p = tree; //遍历 while (top != -1 || p != NULL) { //左孩子入栈 while (p != NULL) { Stack[++top] = p; p = p->left; } //栈不空的时候出栈,并输出栈结点 if (top != -1) { p = Stack[top--]; printf("%c ",p->data); p = p->right; } } } }
后序遍历
void postOrder(Tree *tree) { if (tree != NULL) { //定义两个栈 Tree* Stack1[MAXSIZE]; int top1 = -1; Tree* Stack2[MAXSIZE]; int top2 = -1; Tree* p = NULL; Stack1[++top1] = tree; while (top1 != -1) { p = Stack1[top1--]; Stack2[++top2] = p; if (p -> left != NULL) { Stack1[++top1] = p->left; } if (p -> right != NULL) { Stack1[++top1] = p->right; } } while (top2 != -1) { p = Stack2[top2--]; printf("%c ",p->data); } } }
最后奉上完整代码
#include<stdio.h> #include<stdlib.h> #define MAXSIZE 100 typedef struct BinaryNode { char data; //数据域 struct BinaryNode* left; //指针域 左孩子 struct BinaryNode* right; //指针域 右孩子 }Tree; //赋值 Tree* getTree(char data) { Tree* tree = (Tree*)malloc(sizeof(Tree)); tree->data = data; tree->left = NULL; tree->right = NULL; return tree; } //先序遍历 void preOrder(Tree* btn) { if (btn != NULL) { //定义一个栈 Tree* Stack[MAXSIZE]; //初始化栈 int top = -1; Tree* p; //根节点入栈 Stack[++top] = btn; //栈空循环退出,遍历结束 while (top != -1) { //出栈并输出栈顶结点 p = Stack[top--]; printf("%c ", p->data); //栈是先进后出的,所以先让右孩子进去,再进左孩子 //等下出来的时候.就是左孩子先出来,右孩子后出来 //栈顶结点的右孩子存在,则右孩子入栈 if (p->right != NULL) { Stack[++top] = p->right; } //栈顶结点的左孩子存在,则左孩子入栈 if (p->left != NULL) { Stack[++top] = p->left; } } } } //中序遍历 void InOrder(Tree *tree) { if (tree != NULL) { Tree* Stack[MAXSIZE]; int top = -1; Tree* p; p = tree; //遍历 while (top != -1 || p != NULL) { //左孩子入栈 while (p != NULL) { Stack[++top] = p; p = p->left; } //栈不空的时候出栈,并输出栈结点 if (top != -1) { p = Stack[top--]; printf("%c ",p->data); p = p->right; } } } } //后序遍历 void postOrder(Tree *tree) { if (tree != NULL) { //定义两个栈 Tree* Stack1[MAXSIZE]; int top1 = -1; Tree* Stack2[MAXSIZE]; int top2 = -1; Tree* p = NULL; Stack1[++top1] = tree; while (top1 != -1) { p = Stack1[top1--]; Stack2[++top2] = p; if (p -> left != NULL) { Stack1[++top1] = p->left; } if (p -> right != NULL) { Stack1[++top1] = p->right; } } while (top2 != -1) { p = Stack2[top2--]; printf("%c ",p->data); } } } int main(int argc, char* argv[]) { //搭建图中的二叉树 Tree* tree = (Tree*)malloc(sizeof(Tree)); tree = getTree('A'); tree->left = getTree('B'); tree->right = getTree('C'); tree->left->left = getTree('D'); tree->left->right = getTree('E'); tree->left->left->left = getTree('H'); tree->left->left->right = getTree('I'); tree->left->right->left = getTree('J'); tree->left->right->right = getTree('K'); tree->right->left = getTree('F'); tree->right->right = getTree('G'); printf("先序遍历结果: "); preOrder(tree); printf("nn中序遍历结果: "); InOrder(tree); printf("nn后序遍历结果: "); postOrder(tree); getchar(); return 0; }
本网页所有视频内容由 imoviebox边看边下-网页视频下载, iurlBox网页地址收藏管理器 下载并得到。
ImovieBox网页视频下载器 下载地址: ImovieBox网页视频下载器-最新版本下载
本文章由: imapbox邮箱云存储,邮箱网盘,ImageBox 图片批量下载器,网页图片批量下载专家,网页图片批量下载器,获取到文章图片,imoviebox网页视频批量下载器,下载视频内容,为您提供.
阅读和此文章类似的: 全球云计算
 官方软件产品操作指南 (170)
官方软件产品操作指南 (170)